2.1 – Polar Form

The basics of this chapter on complex numbers should have been covered in Mathematics T. So while I explain stuff over here, I assume that you already know the following about complex numbers:

a. understand what is the real part, imaginary part, and conjugate of a complex number
b. find the modulus and argument of a complex number
c. represent complex numbers geometrically by means of an Argand diagram
d. use the condition for the equality of two complex numbers
e. carry out elementary operations on complex numbers expressed in Cartesian form

So in this post, I’ll be introducing to you another 2 forms of which you can represent a complex number. This will be a short one.

---

You still remember that the modulus of a complex number, a + bi is denoted by |z|, which has the value √(a² + b²). And then, you also remember that the argument of a complex number, denoted by arg z, has the value of tan^-1 (b / a), putting in account which quadrant is the complex number in the Argand diagram. So with the modulus and argument, you can represent a complex number in polar form, or (r, θ) form, which is

|z| (cos (arg z) + i sin (arg z))

For example, the modulus of the complex number –3 + 3i is 3√2, its argument is 3π/4, so its polar form is 3√2 [ cos (3π/4) + i sin (3π/4)]. Using this form will give us a lot of advantages, especially when we learn de Moivre’s theorem in the next post.

Another way of expressing complex numbers using the argument and modulus is the exponential form. The term cos θ + i sin θ can be written as e^iθ, where e is the natural exponent. So by multiplying the modulus in the front of both terms, and substituting the θ with the argument, you get another form of complex numbers! Using the example above, the exponential form of –3 + 3i is 3√2e^i(3π/4). This is something like a compressed form of complex numbers. By now you will be puzzled as in how do you relate cosine and sine with exponents. Well, I’ll show the derivation, only in the chapter Power Series. As for now, just take it as it is. (Extra info: go google for “Euler’s Equation”. You will be surprised by the equation e^iπ + 1 = 0 !)

---

Now that we know 2 extra forms of complex numbers, we want to know how multiplication and division of complex numbers can be done easily in these 2 forms. The general rule is this:
When you multiply 2 complex numbers, you multiply their modulus and add up their arguments. But when you divide 2 complex numbers, you divide their modulus and subtract their arguments.

Let’s give it a try. Suppose we multiply 2 complex numbers, –3 + 3i and –1 – i. You will have:
3√2 [ cos (3π/4) + i sin (3π/4)] × √2 [ cos (3π/4) - i sin (3π/4)] = 6
Did you catch my working? Try using some trigonometry formulas, you will eventually get the answer. Take note that 3π/4 - 3π/4 = 0!
There’s also another way of going about it. Let’s try using the exponential form:
3√2e^i(3π/4) × √2e^i(-3π/4) = 6

This is multiplication. It will be the same for division, go ahead and give it a try. There’s no shortcut for addition and subtraction though, so it’s better to use the cartesian form to solve them.

---

Now we will learn the geometrical effects of basic operations on complex numbers. We will be using the Argand diagram (which I assume you already know what it is, and what are its axes).

1. Conjugation

Basically what conjugation does is that it reflects a complex number across the real axis. Try visualizing these complex numbers as vectors, and you will understand more.

2. Addition & Subtraction

The diagram above shows the addition of 1 + 1i with 1 – 1i. As you can see, it is merely a vector addition, you add up the two of the complex numbers as if they were vectors. You should be able to deduce that for subtraction, just by using the fact that the added minus sign switches the direction of the arrow, you will be able to get the answer, which will be 2i, lying on the imaginary axis. Quite straightforward right?

3. Multiplication & Division

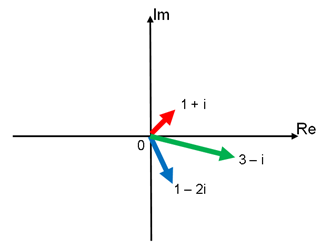
Possibly you couldn’t catch what the diagram meant. The green arrow, 3 – i is the result of the multiplication of 1 + i and 1 – 2i. What happens here is just exactly what we learnt above: the modulus multiplies (the length does not add up, but multiplies as in √2 × √5 = √10) and the argument adds up (0.25π rad – 0.35π rad = –0.1π rad). You can try expressing the complex numbers in polar form, which will help you to identify it clearer. These are really simple stuff, because your head will start to spin when the loci of complex numbers come in.

---

That’s all for this section. Do more exercises on converting complex numbers from the Cartesian form to the polar form. We’ll proceed to unleashing the power of de Moivre’s theorem on the polar form of complex numbers! ☺