A proposition is a declarative sentence that is either true or false, but not both. Normally, we will use the letters p, q and r to represent a proposition. The negation of a proposition is its opposite. For example, if p: 2 + 3 = 5, then its negation is 2 + 3 ≠ 5. A negation of p can be represented by ~p, p̅ or ¬p. It is recommended that you stick to one, so I will be using ~p throughout this post.
Given 2 propositions p and q, a conjunction has the meaning of 'p and q'. Symbolically, it can be written as p ∧ q.
A disjunction has the meaning of 'p or q'. Symbolically, it can be written as p ∨ q. There are some other disjunctions which we don’t normally use, like the 'exclusive or' (p ⊕ q), 'not and' (nand, p | q) and 'nor' (p ↓ q).
An implication is a conditional statement, where p is the antecedent (hypothesis or premise) while q is the consequence (or conclusion). It has the meaning ‘if p, then q’. Symbolically, it can be written as p → q. In English, there are many ways you can interpret this other than ‘if p, then q’. Examples are
- If p, q.
- q unless not p.
- p implies q.
- p is sufficient for q.
- p only if q.
- q when p.
- q if p.
- q whatever p.
- A necessary condition of p is q.
- A sufficient condition of q is p.
- q is necessary for p.
- q follows from p.
A bi-implication is a bi-conditional statement, which means that the implication and its converse are equivalent. It has the meaning ‘p if and only if q’. Symbolically, it can be written as p ↔ q. Other ways of saying it are
- p is necessary and sufficient for q.
- If p then q, and conversely.
- p iff q.
Now using a conditional statement p → q,
- A converse of the statement is q → p.
- An inverse of the statement is ~p → ~q.
- A contrapositive of the statement is ~q → ~p.
To further elaborate the meanings of all the stuff above, I’ll continue by introducing truth tables.
TRUTH TABLES
A truth table is a table which states the truth values of various statements. Here, ‘T’ means ‘true’, while ‘F’ means ‘false’. So the truth table for negation is
| p | p̅ |
|---|---|
| T | F |
| F | T |
which means that every time when p is true, p̅ is false and whenever p is false, p̅ is true.
Let’s go on for conjunctions, disjunctions, implications and bi-implications:
| p | q | p ∧ q | p ∨ q | p → q | p ↔ q |
|---|---|---|---|---|---|
| T | T | T | T | T | T |
| T | F | F | T | F | F |
| F | T | F | T | T | F |
| F | F | F | F | T | T |
Summarising the results above,
- p ∧ q is true if both p and q are true;
- p ∨ q is true if either one of p or q is true;
- p ↔ q is true if both p and q are true, or both p and q are false;
- p → q is a little tricky: it is only false when p is true and q is false.
To further understand the results of p →q, let's use an illustration. Suppose a certain political party in Malaysia gives a conditional statement: “If we win the next elections, we will immediately reduce the price of petrol by 20%.” So according to their statement, there will be two outcomes:
Situation 1: They won the elections
In the event that they really did reduce the petrol price, then the statement is true. But if they break their promise and the petrol price isn’t reduced, then the statement is false.
Situation 2: They lost the elections
Since they didn’t promise anything about what they will do if they lost, whatever that happens, be it the price of petrol increases, remains or reduces, doesn’t make the statement false, and so therefore, for either case, the statement is true.
Now we’ll go on to see the truth tables for converse, inverse and contrapositive:
| p |
q |
p → q |
q → p (Converse) |
~p → ~q (Inverse) |
~q → ~p (Contrapositive) |
|---|---|---|---|---|---|
| T | T | T | T | T | T |
| T | F | F | T | T | F |
| F | T | T | F | F | T |
| F | F | T | T | T | T |
Notice that the converse is equivalent to the inverse! Besides, the statement itself is equivalent to its contrapositive. This is a very important piece of information when studying logic.
PRECEDENCE
In problem solving, you can combine all the logical operators to make a very complicated statement. For example, you can have
[ (~r ∧ ~p) → q ] ∧ [ q → (~r ∨ ~p) ]
In order to understand the statement, you need to have a precedence of logical operators, which means, which symbol comes first and which comes second and so on. The precedence of logical operators, from first to last is as follows: ~, ∧,∨,→,↔.
If 2 statements have the same truth values, we say that the statements are logically equivalent. if p and q are logically equivalent, we write p ≡ q. Note that it is an equal sign with 3 strokes instead of 2.
A tautology is a compound proposition that is always true, no matter what the truth values of the propositions that occur in. For example, ~p → (p → q) is a tautology. You can check by looking at its truth table below:
Opposite to a tautology is a contradiction, a compound proposition that is always false. A contingency is neither a tautology or a contradiction.
Here are some common laws of logic and some notes identities that you should memorize:
Some laws for bi-conditional statements:
PREDICATION & QUANTIFICATION
Sometimes, we can use predicates to represent a logic statement, which depends on an unknown, or various unknowns. A predicate is normally denoted by P(x), or any capital letter followed by a bracket with an unknown in it. For example, C(x) may represent “x is a comedian” while F(x) may represent “x is funny”.
A quantifier is used to generalise or specialize a particular predicate, and is placed in front of it. There are 2 kinds of quantifiers:
1. The universal quantifier, denoted by ∀xP(x) which means ‘for all x, P(x)’. It also could mean ‘for every’, ‘all of’, ‘for each’, ‘given any’, ‘for arbitrary’ or ‘for any’. In terms of P(x), it can be represented by the logical statement
which means the conjunction of any variable in the predicate P. Using the example above, if x means ‘people’, then ∀xC(x) means ‘everyone is a comedian’.
2. The existential quantifier, denoted by ∃xP(x) which means ‘for some x, P(x)’. It also could mean ‘at least one’, ‘there is a…’ or ’there exists’. In terms of P(x), it can be represented by the logical statement
which means that it is the disjunction of any variable in the predicate P. Again, using the example above, ƎxC(x) means ‘some people are comedians’. Sometimes, you might also see the expression Ǝ!xC(x). Instead of ‘for some x’, this means ‘there is exactly one x’. We call it the uniqueness quantifier.
We use these quantifiers just the same way how we use those p’s and q’s earlier on, you can add the negating sign (~) or the conditional arrows (↔ and →) to them. So what are the truth values of these quantifiers?
The statement ∀xP(x) is TRUE if P(x) is true for all x, in which x should belong to a particular domain (people, animal, students or etc). It is FALSE if we could find an x in which P(x) is false. Using the same example again, ∀xC(x) is true if every human being is a comedian, but is false if you could find one person (yes, you only need one person) who isn’t a comedian.
The statement ƎxP(x) is TRUE if there exist one x which is true, and is FALSE if every x is false for P(x). Using the same example, ƎxC(x) is true if there is one human being on earth is a comedian, but is false if you can’t find a single human being who is a comedian.
Simple? Let me give you some common rules for quantifiers:
This one tells you how you can bring the quantifier into the brackets. Beware though, you can’t bring a universal quantifier in if you use a disjunction, and the same applies to the existential quantifier and conjunctions.
The negations of quantifiers:
This is quite straightforward.
A nested quantifier is formed when you use 2 or more quantifiers in 1 predicate. Examples are like
Notice that both quantifiers mean different things. The first one says ‘for all x, there exist a y such that P(x,y) is true’, while the second one says ‘there exist an x such that all y is true for P(x,y)’. Let me give you a detail example:
Let P(x,y) be the statement “x has sent an SMS to y”, where the domain of x and y are ‘students’. We can see that
1. ƎxƎyP(x,y) means “There is some student who sent an SMS to some student.”
2. Ǝx∀yP(x,y) means “There is a student who sent an SMS to all other student.”
3. ∀xƎyP(x,y) means “All students sent an SMS to at least one student.”
4. Ǝy∀xP(x,y) means “There is a student who receives an SMS from all students.”
5. ∀yƎxP(x,y) means “Every student has been sent an SMS by at least a student”
6. ∀x∀yP(x,y) means “All students have sent an SMS to all students.”
Notice that ƎxƎy and ƎyƎx do mean the same thing, and this applies to ∀x∀y and ∀y∀x too, but not the mixture of both. Now the problem is: how do you know the truth values for nested quantifiers? I’ll show you in a table below:

You can actually work it out yourself by using the negating rules stated above. It’s simple: a negation sign passes through a universal quantifier turns into an existential quantifier, and vice versa. Another important remark is this:
"if Ǝx∀yP(x,y) is true, then ∀yƎxP(x,y) is true, but not INVERSELY.”
That’s all for logic. You should practice more on translating sentences into logical statements, because it can be very confusing sometimes. Also, practice how to prove the equivalence of logical statements using the given laws. For complicated equivalences (more than 2 propositions), you could use a truth table. It will be faster. We’ll start doing proofs in the next section.



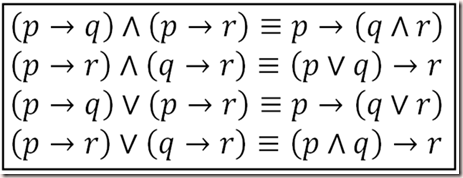
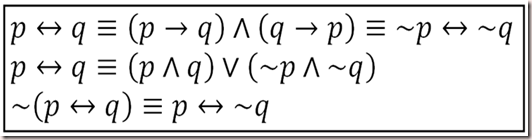
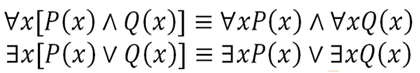
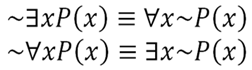
hi, your notes are really good, i can understand but i still cant solve the past year problems in simplify the complicated logics, can u give me some examples and sample answer? thanks.
ReplyDeleteIf you are commenting on this page, I suppose you want some examples on quantifiers, right? Which past year paper question are you refering to? I can't recall that quantifiers came out in the past year papers...
ReplyDelete1. Find the contrapositive, converse, inverse and negation of the quantifier proposition
ReplyDelete∀x∈R ,if x(x+1)>0 ,then, x >0 or x <−1.
I believe you could have identified that p is x(x+1)>0, and q is x> 0, r is x<-1. You get ∀x∈R, p → (q V r). The contrapositive, converse and inverse are done to the conditional statement without altering the quantifiers, that means, it is still ∀x∈R. But the negation does change it to Ǝx∈R, ~ [p → (q V r)]. Hope that does help a little. :)
ReplyDeletehi, can i ask you some questions from past year exam? How to simplify pV(~pVq)V(~pV~q)?
ReplyDeletecheck on internet
Delete