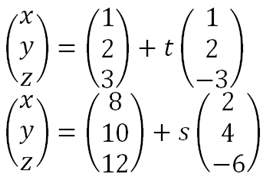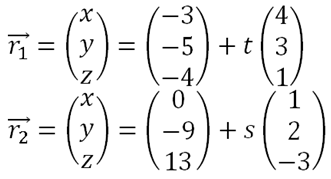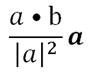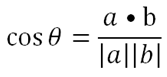12.3 – Planes

A plane is simply just a flat surface in space. We first start by introducing the vector equation of a plane,

where a is a position vector, and b and c are 2 non-parallel vectors, s and t being 2 arbitrary constants. Consider the diagram below,

We need to have at least 2 direction vectors to show the direction of the plane, and then a point to know where does the plane lie exactly. We multiply the 2 direction vectors with different constants, to show that any direction vector proportion to that ratio is also a direction vector. Similarly, this form of the plane equation is not unique. Again, this form can be written in the ijk form, in which looks ugly and long.

There is another vector equation of the plane. Though not named properly, I call it the ‘normal’ form. We first find the normal vector of a plane, i.e., a vector which is normal to both the direction vectors. You obtain the normal vector by getting the cross product of b and c. Suppose that the normal vector is (a, b, c), the normal form of the equation will be

Where d is constant which determines the position of the plane. d has a significant meaning. If the normal vector (a, b, c) is a unit vector (magnitude = 1), then d is the perpendicular distance from the plane to the origin. For 2 planes, if their values of d have opposite signs, it means that they are at the opposite sides of the origin. Finding the value d is simple: Just plug in a point lying in the plane into x, y, z, then you get it.

If we evaluate the dot product above, we get the cartesian form,

This cartesian form is unique, unlike the other forms. This is the most common form of the equation of planes used. You can see that this equation is linear, and that the equation
y = mx + c, or x = a are all equations of planes in 3 dimensional space.

So to sum up, to construct a plane equation, you need one of these information:
1. 3 points lying on the plane.
2. 2 points lying on the plane, and 1 directional vector.
3. 2 lines lying on the plane.
4. a point lying on the plane, and the normal vector of a plane.

There is a fast way to get the equation of the plane when 3 points are given. I haven’t tried this before, but you could make use of the determinants below to find your equation:

---

LINE LIES IN / PARALLEL / INTERSECT A PLANE

We shall now discuss how to determine whether a line lies in / is parallel to / intersects a plane. Given the equations of the line and plane to be

We first find whether the direction vector of the line is parallel to the plane. In other words, we want to know whether the direction vector of the line is perpendicular to the normal vector of the plane. By taking b • n, if the answer is zero, then the line is parallel to the plane. We might want to know whether the parallel line actually lies in the plane. We can do this by substituting the position vector of the line into r₂,  and if LHS = RHS, then indeed the line lies in the plane, and is otherwise if the equality doesn’t hold.

So if b • n ≠ 0, this means that the line definitely intersects the plane. The point of intersection can be found by letting r₁ = r₂, that is,

You should be able to solve for t, which satisfies all the 3 parametric equations. Then finally, to find the point of intersection, we substitute t back into the line equation to find (x, y, z).

---

PLANE PARALLEL TO / INTERSECTS ANOTHER PLANE

Since the cartesian equation is unique, 2 planes can only coincide one another if they have the same plane equation. 2 planes are parallel only if they have the same normal vector, which is also easy to find. Planes that are not parallel have to intersect somewhere, and we can determine the line of intersection. Consider 2 plane equations below:

We first find the common direction by using

this will be the direction vector of the intersecting line. To find a position vector of the line, we make use of the cartesian equation of both planes,

We need to solve this system of linear equations to find x, y and z. Recall the Chapter on Matrices, this system of equations have infinitely many solutions. As usual, let one of them be t, solve for x, y and z in terms of t, and then just substitute a value for t to get a random position vector. The line equation is thus found.

---

DISTANCE FROM A POINT / PARALLEL LINE TO A PLANE

I think I won’t prove this one, as it is similar to the proof in 2D. To find the distance between a point (x, y, z) to a plane, make use of the equation in your Data Booklet:

Notice that there is something different in my equation. It is ‘-d’ instead of ‘+d’ because I made use of the cartesian equation ax + by + cz = d instead of ax + by + cz + d = 0. Please DO NOT CONFUSE THEM.

If you want to find the distance between a parallel line to the plane (note that the line has to be ‘parallel’ to have a ‘distance’…), you substitute the position vector of the line (x, y, z) into the above equation, and you get it.

---

DISTANCE BETWEEN 2 PLANES

Given 2 parallel planes,

We can find the distance between them by finding

I will explain why this makes sense. Firstly, you should recall that the values d/|n| and e/|n| are the perpendicular distances from the planes to the origin. Also remembering that the distance really depends on whether both the planes lie on the same side of the origin, or the other (same sign or different sign). You subtract them, then take the modulus because distance is never negative.

---

ANGLE BETWEEN LINE AND PLANE

Consider a line with direction vector a and a plane with normal vector n. The angle between the line and the plane can be found by using the equation

Note that if you used cos θ, you would have gotten the angle between the line and the normal vector instead.

---

ANGLE BETWEEN PLANES

The angle between 2 planes is actually the same angle between the 2 normal vectors. So given 2 planes with normal vectors m and n respectively, we can find the angle between 2 planes by using the dot product,

Recall that this is the same formula to find the angle between 2 lines.

---

Now that you know how to construct planes, you might be curious as in how 3D shapes are constructed. Again, you could make use of the applet I shared with you in the previous post, from the drop down menu of new graph, choose z = f(x, y) surfaces. Fiddle around it and have fun creating awkward shapes. This is obviously out of your syllabus, but let me just give you some equations for some very common shapes in 3D:

  
           cylinders,                  elliptic paraboloid,                  hyperbolic paraboloid,
          x² + y² = r²                        z = x² + y²                                     z = x² – y²

  
                           ellipsoid,                                    elliptic cone,                    hyperboloid
                  ax² + by² + cz² = 1                           x² + y² – z² = 0                x² + y² – z² = 1

---

End of all those hard core Mathematics, at last! The next few chapters will be on Statistics, and so life will be much easier thereafter. ☺

12.2 – Straight Lines

Straight lines in 3 dimensions isn’t as easy as it is in 2 dimensions. When we want to construct a straight line in space, it must be pointing at a specific direction, and you must give at least one point that it passes through.

---

EQUATION OF A LINE

Let r be a line in xyz space, we let a and b be 2 vectors and t be an arbitrary constant. The vector equation of a line can be represented by the equation

The vector a (x₀, y₀, z₀) is a position vector. It is a point in space in which the line passes through. Then the vector b is a direction vector. This vector determines the direction of the line. The constant t is there, meaning that any scalar multiplication of the direction vector, is also the same direction vector. Summarizing it up, you actually get this:

You need some visualization here. Look at the diagram below. The green line L first needs a point a in space. Then you need a direction vector b to tell you where the line extends too. So if you analyse carefully, an equation of a line is not unique. You can put in an infinite amount of different position vectors, or use an infinite amount of direction vectors of the same ratio to construct different line equations, which actually refers to the same line. This is unlike lines in 2D, where a line only has one representation.

You might have also noticed that the vector equation of a line is actually a parametric equation of a line. If you break it down,

This is where is the position vector a, and is the direction vector b. Probably now you figure out why the line is not unique, since parametric equations are not unique. By the way, we can also write the vector equation as r = ai + bj +ck + t(pi + qj + rk). I don’t like this method as we waste too much time writing the ijk’s and +/- signs.

Now if we try to modify the 3 parametric equation, such that it is t in terms of something else, we get the cartesian equation, as below:

We normally write this whole chunk of equalities without the ‘=t’, I only show it here for clarity. A line in 3D space has 2 equal signs. So what if p, or q, or both are 0? An example of such lines are

You might want to substitute it back into the vector equation to check this out. You probably could have guessed why we prefer to use the vector equation instead of the cartesian equation. WIth all these information, you should be able to know how to construct a line equation, given only 2 points it passes through.

---

SKEW, PARALLEL, INTERSECT?

In 2D, lines are either parallel to each other, or they intersect. However in 3D, there exist another relationship between 2 lines, in which they do not intersect and are not parallel to each other. These lines are called skewed lines.

Our question is this: how do we show that whether 2 lines are parallel, intersect one another, or are skewed?

To show that 2 lines are parallel, we show that they have the same direction vector. The 2 lines below

are parallel, because they have the same direction vector. You can further check whether the lines coincide (or, whether they are just both the same line). To do this, we take the point (1, 2, 3) and substitute into (x, y, z) in the second equation. Doing some algebra, we find that the value of s for the 3 parametric equations are not consistent. Therefore, it does not coincide, and is a parallel line. This method also tells us whether a particular point lies in the line. So here we see that the point (1, 2, 3) does not lie in the second line.

To show that 2 lines intersect, we let line 1 equal line 2. We get 3 equations. Consider the two lines below:

We have

-3 + 4t = s
-5 + 3t = -9 + 2s
-4 + t = 13 – 3s

If we could find a value of s and t such that it satisfies all the 3 equations, the lines intersect. If the value of s and t contradict one another, then the lines are skewed. We can further find the point of intersection. By using the values of s and t, substituting them back into the initial equations, we get the intersection point. In this case, the point of intersection is
(5, 1, –2).

---

DISTANCE FROM POINT TO LINE

Given a line r₁ and point r₂,

to find the distance from the point to the line, we want to make use of the sine of the angle between the line r₁ and the line (r₂ – a). Look at the diagram below.

Recalling that |a × b| = |a||b| sin θ, the distance between the line and the point r₂ is

---

DISTANCE BETWEEN 2 LINES

To find the distance between 2 lines, we have 2 situations:

1. the lines are parallel

Given the two lines, we can make use of what we learnt from the part above, and find that the distance between these 2 lines are just

2. the lines are skewed

Given 2 lines, the shortest distance between 2 skewed lines can be found through the equation

where k is a constant. Let me explain this a little. The distance between the two lines is r₂ – r₂. It is parallel to the normal vector (b × d), and that is why we multiply it with k. So after setting up the equation, we get the equation c + sd – a – tb = k(b × d), which is actually 3 parametric equations in terms of 3 variables t, s and k. From here, we solve for s, t and k, and we multiply k to the magnitude of b × d,

and thus you get the shortest distance between 2 skewed lines.

---

ANGLE BETWEEN 2 LINES

Recalling the formula you learnt in the previous section,

You use this formula to find the angle between two lines, by substituting a and b as the direction vectors of both lines. Shouldn’t be a problem for you, I think.

---

Straight lines are pretty easy to draw in 3 dimensions, but have you ever how does a curve in 3D look like? You can plot a 3D curve by changing the variables of in the parametric equation. Here is an applet for you to try out. In the drop down menu new graph, choose parametric curve. Then beside the columns x(t), y(t) and z(t), just put in whatever function you can think of. Then you will see how a curve in 3D looks like. Fiddle around with it, put a frame or etc for better reference. 3D curves are not in your syllabus, so don’t worry. ☺

12.1 – 3D Vectors

This chapter will be a continuation and combination of what you learnt from the chapters Coordinate Geometry and Vectors. As we come into 3 dimensions, we make use of vectors as it makes our analysis much easier. Here, we introduce the coordinate systems for three-dimensional space ℝ². The study of 3-dimensional spaces lead us to the setting for our study of calculus of functions of two and three variables later in University.

We set up the 3D coordinate system by fixing a point O in space (called the origin) and take three lines passing through O that are perpendicular to each other. These lines are labelled as x-axis, y-axis and z-axis respectively. The direction of the z-axis is determined by the right-hand rule:

I think you should be familiar with this rule in Physics. When your fingers point in the direction in the x-axis, and make it curl towards the y-axis, then your thumb will be pointing to the z-axis. Try to get used to this setting: with the z-axis pointing upwards, x on the left, y on the right.

A point P in space can be represented by an ordered triple (a, b, c) where a, b and c are projections of the point P onto the x-, y- and z-axis respectively. The three dimensional space is also called the xyz-space.

You probably should know how we represent a vector in 3D. Using the same conventions of unit vectors i and j, we just add one more k to represent the unit vector in the z direction (e.g., 2i + 3j – 5k). Everything about a vector in 2D works about the same in 3D. The length of a vector P(a, b, c) follows the Pythagorean relation

And similarly, the distance between 2 position vectors A and B can be found by the equation

Let’s do a little revision on the properties of vectors, scalar multiplication, addition, subtraction & etc. We let a, b and c be 3 vectors, k and h be 2 constants, then we have

(1) a + b = b + a
(2) a + (b + c) = (a + b) + c
(3) a + 0 = a
(4) a + (–a) = 0
(5) k(a + b) = ka + kb
(6) (k + h)a = ka + ha
(7) (kh)a = k(ha)
(8) 1a = a

---

SCALAR PRODUCT

Scalar product, also known as the dot product, is a multiplication of 2 vectors (a, b, c) and (d, e, f) such that

The scalar product yields an answer in the form of a scalar, which is a value instead of a vector. In trigonometry, it can be represented by the equation
a • b = |a||b| cos θ

I believe all these are not new to you, as you have studied it in Maths T. However, in this section, we will be going quite detail on the algebra of vectors, unlike in Maths T where you focused more on the applications, namely the resultant force / velocity and relative velocity. Let us look at the properties of scalar products. Given a, b and c are vectors, d being a constant, we have

(i) a • b = b • a (commutativity)
(ii) a • (b + c) = a • b + a • c (distributive law)
(iii) (da) • b = d(a • b) = a • (db)
(iv) 0 • a = 0
(v) a • a = |a|²

We say that two vectors are orthogonal to each other when they are perpendicular to each other. Two vectors a and b are orthogonal if and only if a • b = 0. In 3D, we say that a vector a is orthogonal to vectors b and c if a is perpendicular to both b and c.

The component of b onto a (or scalar projection) is the resolved part of a in the direction of b. This means that when we have 2 vectors a and b pointing at 2 different directions, with their tail of the arrow connected to each other, the component of b onto a is the length of the orthogonal projection of b onto a.

We write the notation comp_a b to represent the component of b onto a, and mathematically, it has the value
 
and according to the picture above, it is the length of PS.

The vector projection of b onto a is just the vector PS itself. it has the formula

We write the notation proj_a b to represent the projection of b onto a. Remember that the answer is a VECTOR, not just a VALUE.

For a vector a (a_i, a_j, a_k), The direction ratio is written as a_i : a_j : a_k, whereby your answer could be in the simplest form (divided by its highest common divisor). The direction cosines of the vector a are
 
respectively.

The angle between the vector and the z-axis can be found using the equation

and therefore you can deduce the angle between the vector and the x-axis & y-axis respectively.

Recalling that the dot product of 2 vectors, a • b = |a||b| cos θ, we can easily find the angle between 2 vectors,

---

VECTOR PRODUCT

Also known as cross product, the vector product is something new for you, as it cannot exist in a 2D plane. We define the vector product of 2 vectors (a, b, c) and (d, e, f) to be

The cross product yields a vector (it has a magnitude and a direction), which is orthogonal to both the original vectors. In trigonometry, the cross product a × b = |a||b| sin θ.

You can use the right hand rule to determine the direction of the cross product. Point your fingers to the direction of a, curl it towards the direction of b, then your thumb points in the direction of a × b. This information is very important we come to the section on planes.

Different from the dot product, any vector cross itself yields zero.
ḭ × ḭ = 0, j̰ × j̰ = 0, k̰ × k̰ = 0

Or in other words, the cross product of 2 parallel vectors is zero. You can use your right hand rule to verify this. For the unit vectors, you could also get the following results:

We shall now see the properties of the cross product. If a, b and c are vectors and d is a scalar, then

(i) a × b = –b × a
(ii) (da) × b = d(a × b) = a × (db)
(iii) a × (b + c) = a × b + a × c
(iv) (a + b) × c = a × c + b × c
(v) a • (b × c) = (a × b) • c
(vi) a × (b × c) = (a • c)b – (a • b)c
(vii) (a × b) • a = 0

Probably (vi) is hard to remember. (vii) is just the definition of the dot product, where the dot product of 2 orthogonal vectors equals to zero. Also take note that the cross product is not commutative. Reversing the a’s and b’s will result in an extra minus sign.

The cross product has many applications, especially in physics. You use the cross product to find the torque, magnetic force and etc. In geometry, we see that the area of a triangle  made up by 3 vectors a, b and c is

A scalar triple product of vectors a, b and c is a • b × c. If you might have noticed, you have to do the cross product first before the dot product. If  you did the dot product first, then you get a scalar crossing a vector, in which by definition, does not exist. Note also that a • b × c = a × b • c. We could evaluate a • b × c using determinant

Where a = (a₁, a₂, a₃), b = (b₁, b₂, b₃), and c = (c₁, c₂, c₃) respectively. We use the scalar triple product to find the volumes of various solids. Since b × c is the base area of a solid, when dotted with another vector a, it multiplies the area with the cosine of the height. So the formulas for different solids are as below:

1. volume of cuboid & parallelogram:
a • b × c

2. volume of tetrahedron:

3. volume of triangular prism

4. volume of pyramid

---

Not really hard I think. You might probably be asked to simplify an equation by making use of the properties of the cross and dot products. Get used to them, you will use them for the next two sections! ☺