Straight lines in 3 dimensions isn’t as easy as it is in 2 dimensions. When we want to construct a straight line in space, it must be pointing at a specific direction, and you must give at least one point that it passes through.
EQUATION OF A LINE
Let r be a line in xyz space, we let a and b be 2 vectors and t be an arbitrary constant. The vector equation of a line can be represented by the equation
The vector a (x0, y0, z0) is a position vector. It is a point in space in which the line passes through. Then the vector b is a direction vector. This vector determines the direction of the line. The constant t is there, meaning that any scalar multiplication of the direction vector, is also the same direction vector. Summarizing it up, you actually get this:
You need some visualization here. Look at the diagram below. The green line L first needs a point a in space. Then you need a direction vector b to tell you where the line extends too. So if you analyse carefully, an equation of a line is not unique. You can put in an infinite amount of different position vectors, or use an infinite amount of direction vectors of the same ratio to construct different line equations, which actually refers to the same line. This is unlike lines in 2D, where a line only has one representation.
You might have also noticed that the vector equation of a line is actually a parametric equation of a line. If you break it down,
This is where 
is the position vector a, and 
is the direction vector b. Probably now you figure out why the line is not unique, since parametric equations are not unique. By the way, we can also write the vector equation as r = ai + bj +ck + t(pi + qj + rk). I don’t like this method as we waste too much time writing the ijk’s and +/- signs.
Now if we try to modify the 3 parametric equation, such that it is t in terms of something else, we get the cartesian equation, as below:
We normally write this whole chunk of equalities without the ‘=t’, I only show it here for clarity. A line in 3D space has 2 equal signs. So what if p, or q, or both are 0? An example of such lines are
You might want to substitute it back into the vector equation to check this out. You probably could have guessed why we prefer to use the vector equation instead of the cartesian equation. WIth all these information, you should be able to know how to construct a line equation, given only 2 points it passes through.
SKEW, PARALLEL, INTERSECT?
In 2D, lines are either parallel to each other, or they intersect. However in 3D, there exist another relationship between 2 lines, in which they do not intersect and are not parallel to each other. These lines are called skewed lines.
Our question is this: how do we show that whether 2 lines are parallel, intersect one another, or are skewed?
To show that 2 lines are parallel, we show that they have the same direction vector. The 2 lines below
are parallel, because they have the same direction vector. You can further check whether the lines coincide (or, whether they are just both the same line). To do this, we take the point (1, 2, 3) and substitute into (x, y, z) in the second equation. Doing some algebra, we find that the value of s for the 3 parametric equations are not consistent. Therefore, it does not coincide, and is a parallel line. This method also tells us whether a particular point lies in the line. So here we see that the point (1, 2, 3) does not lie in the second line.
To show that 2 lines intersect, we let line 1 equal line 2. We get 3 equations. Consider the two lines below:
We have
-3 + 4t = s
-5 + 3t = -9 + 2s
-4 + t = 13 – 3s
If we could find a value of s and t such that it satisfies all the 3 equations, the lines intersect. If the value of s and t contradict one another, then the lines are skewed. We can further find the point of intersection. By using the values of s and t, substituting them back into the initial equations, we get the intersection point. In this case, the point of intersection is
(5, 1, –2).
DISTANCE FROM POINT TO LINE
Given a line r1 and point r2, 
to find the distance from the point to the line, we want to make use of the sine of the angle between the line r1 and the line (r2 – a). Look at the diagram below.
Recalling that |a × b| = |a||b| sin θ, the distance between the line and the point r2 is
DISTANCE BETWEEN 2 LINES
To find the distance between 2 lines, we have 2 situations:
1. the lines are parallel
Given the two lines, we can make use of what we learnt from the part above, and find that the distance between these 2 lines are just
2. the lines are skewed
Given 2 lines, the shortest distance between 2 skewed lines can be found through the equation
where k is a constant. Let me explain this a little. The distance between the two lines is r2 – r2. It is parallel to the normal vector (b × d), and that is why we multiply it with k. So after setting up the equation, we get the equation c + sd – a – tb = k(b × d), which is actually 3 parametric equations in terms of 3 variables t, s and k. From here, we solve for s, t and k, and we multiply k to the magnitude of b × d,
and thus you get the shortest distance between 2 skewed lines.
ANGLE BETWEEN 2 LINES
Recalling the formula you learnt in the previous section,
You use this formula to find the angle between two lines, by substituting a and b as the direction vectors of both lines. Shouldn’t be a problem for you, I think.
Straight lines are pretty easy to draw in 3 dimensions, but have you ever how does a curve in 3D look like? You can plot a 3D curve by changing the variables of in the parametric equation. Here is an applet for you to try out. In the drop down menu new graph, choose parametric curve. Then beside the columns x(t), y(t) and z(t), just put in whatever function you can think of. Then you will see how a curve in 3D looks like. Fiddle around with it, put a frame or etc for better reference. 3D curves are not in your syllabus, so don’t worry. ☺
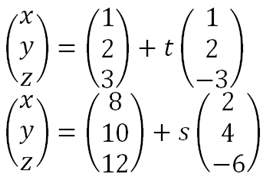
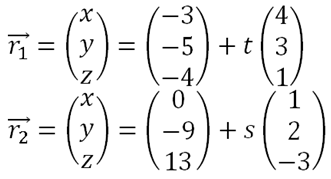
No comments:
Post a Comment