In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A graph, G = (V, E) consists of V, a nonempty set of vertices / nodes and E, a set of edges. In other words, a graph is a discrete structure consisting of vertices, and edges that connect these vertices. Each edge has either one or two vertices associated with it (endpoints). An edge is said to connect its endpoints. A graph looks something like this:
As you can see, a and b are vertices, while e and f are edges. the edge g is called a loop. The vertex set V = {a, b}.
In this section, there will be many terminologies which you should remember, and should be able to write down their definition in your exam. Here we will be learning the different kinds of graphs and their names:
An infinite graph is a graph with infinite vertex set (or rather, an infinite number of vertices). The definition of a finite graph is just the converse. Throughout this section, we will only be learning about graphs with finite amount of edges and vertices.
A simple graph is a graph in which each edge connects two different vertices and where no two edges connect the same pair of vertices. A multigraph is a graph that has multiple edges connected to the same vertices, while a pseudograph is a graph that may include loops, multiple edges connecting the same pair of vertices. The 3 pictures below illustrate a simple graph, a multigraph and a pseudograph:
Notice for the multigraph, there are 2 edges connecting both a to b and a to c, while 3 edges connecting e to f. As for the pseudograph, there exist loops at the vertices e and f.
The complement of the graph, G̅, has the same amount of vertices as graph G but whenever there is a edge between vertices a and b, there won’t be an edge, and whenever there isn’t an edge between vertices a and b, an edge is added to it. This only applies to simple graphs. For example, below is the graph and its complement:
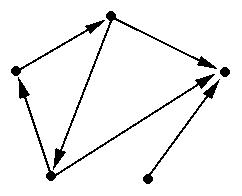
All the above graphs are undirected, that means that one can traverse an edge in both directions. A directed graph (or digraph), consists of a nonempty set of vertices and a set of directed edges (or arcs). Each directed edge is associated with an ordered pair of vertices. The directed edge associated with the ordered pair V = (u, v) is said to start at u and end at v. In other words, we say that u is adjacent to v, while v is adjacent from u. Notice thee different uses of { } and ( ) brackets for undirected and directed graphs. Below is a directed graph:
For the ordered pair of vertices (u, v), we say that u and v are adjacent, and we say that the edge is incident / connects u and v. u is known as the initial vertex and v being the terminal vertex. Using the similar naming convention, we can describe a simple directed graph as a directed graph in which each edge connects two different vertices and where no two edges connect the same pair of vertices. Then similarly, a directed multigraph can be defined.
An underlying undirected graph is the undirected graph that results from ignoring directions of edges. It is just the same graph without the arrows. A mixed graph, is a graph with both directed and undirected edges. A converse of a directed graph, is the graph in which its arrows are reversed.
For every graph, we could come up with subgraphs, which are graphs that are subsets of the initial graph. For example, the graph
can be broken down into 11 subgraphs below:
An exercise for you here is that you can try to figure out whether you can determine the total amount of subgraphs, given the values of V and E.
A bipartite graph is a simple graph such that its vertex set V can be partitioned into 2 disjoint sets V1 and V2 such that every edge in the graph connects a vertex in V1 and V2. Consider the bipartite graph below:
Notice that I coloured the vertices with 2 colours, red and blue. The blue vertices will not connect to any other blue vertex, and the red vertices too, they don’t connect to any other red vertex. The graph is partitioned such that there are two sets or parties of vertices which can be grouped together. To identify a bipartite graph is simple: As long as you can colour adjacent vertices with only 2 colours, then it is a bipartite graph. For example, you colour the first vertex blue. The vertices adjacent to the first vertex must be coloured red, and if you can fit all the vertices with 2 colours such that no two adjacent vertices have the same colour, then it is a bipartite graph. Notice also, that a graph is bipartite if and only if it has no odd cycles. We will learn about cycles in the next session.
Now there are a 5 types of special simple graphs I want to introduce:
1. Complete Graph Kn
This graph is a simple graph that contains exactly 1 edge between each pair of distinct vertices. In other words, this graph has the maximum amount of edges it can have, and adding any edge between any 2 vertices will turn it into a multigraph. The graphs look as follows:
For the K4 graph, it has 4 vertices, and every vertex is connected to the other 3 vertices. By simple calculations, a Kn graph has n vertices, and n(n-2)/2 edges.
2. Cycle Graph Cn
This graph, where n ≥ 3, consists of n vertices and edges.
Strictly speaking, C2 is not a Cycle graph, as n < 3. Notice that every vertex is only connected to two other vertices. It looks like a regular polygon with n sides.
3. Wheel Graph Wn
This graph looks like a wheel with n sides. We obtain the wheel when we add an additional vertex to the cycle Cn, for n ≥ 3, and connect this new vertex to each of the n vertices in Cn, by new edges.
A Cn graph has n + 1 vertices and n 2n edges.
4. n-Dimensional Hypercube, Qn
This graph, also know as n-cube, is the graph whose vertices represent the 2n bit strings of length n. Two vertices are adjacent if and only if the bit strings that they represent differ in exactly one bit position. I don’t think this graph is in the syllabus, but I think it will be good for you to know:
This graph has 2n vertices and 2n-1 edges. Try proving this if you are free.
5. Complete Bipartite Graph, Km,n
This graph is just a bipartite graph, in which there is only 1 edge between each pair of distinct vertices across V1 and V2. Note that the number of edges, | E(m, n) | = mn, and there are m + n vertices.
Now that we know everything about the structure of graphs, we shall now get into the a little calculations. The degree of vertex is the number of edges incident with it, except that a loop at a vertex contributes 2 times to the degree of that vertex. The degree of a vertex is denoted by deg (v). When deg (0), we say that the vertex is isolated, and when deg (1), then we say that the vertex is pendant.
We now want to find the relationship between the sum of degrees of vertices & number of edges. The Handshaking Theorem states that the sum of degree of vertices is double the amount of edges. In equation form, we have
This theorem has many implications. One of them is that we know that a graph cannot exist if the sum of degree of vertex is odd.
In the case for directed graphs, we denote deg+ (v) as the out-degree, meaning the amount of arcs pointing away from the vertex, while the in-degree is denoted by deg- (v), which is the amount of arcs pointing towards the vertex. Modifying the handshaking theorem, we have
This section isn’t really hard. You just need to remember the definitions of the graphs. Take note that these graphs need not to be drawn on graph paper. Just draw them in the test pad given to you in exams. ☺










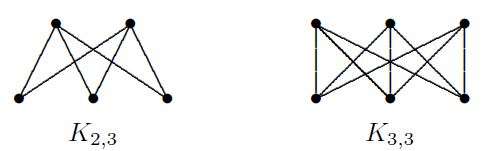


Thanks for all the contents !
ReplyDeleteIsn't the labeling for the Wheel graph in the image: http://lh4.ggpht.com/-KTYjggkIXQg/Thvi9nuKWbI/AAAAAAAAAi4/eLkaJaLk9u0/s1600-h/image18.png supposed to be
ReplyDeleteW4, W5, W6, and W7 in that order?
Hi, sorry I didn't get to reply your question earlier, and I couldn't access the image either... Hope you found your solution! :)
Delete