This chapter will be a continuation and combination of what you learnt from the chapters Coordinate Geometry and Vectors. As we come into 3 dimensions, we make use of vectors as it makes our analysis much easier. Here, we introduce the coordinate systems for three-dimensional space ℝ2. The study of 3-dimensional spaces lead us to the setting for our study of calculus of functions of two and three variables later in University.
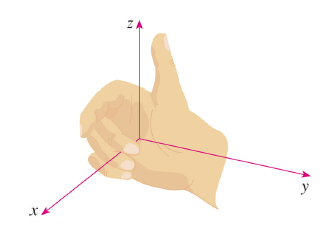
We set up the 3D coordinate system by fixing a point O in space (called the origin) and take three lines passing through O that are perpendicular to each other. These lines are labelled as x-axis, y-axis and z-axis respectively. The direction of the z-axis is determined by the right-hand rule:
I think you should be familiar with this rule in Physics. When your fingers point in the direction in the x-axis, and make it curl towards the y-axis, then your thumb will be pointing to the z-axis. Try to get used to this setting: with the z-axis pointing upwards, x on the left, y on the right.
A point P in space can be represented by an ordered triple (a, b, c) where a, b and c are projections of the point P onto the x-, y- and z-axis respectively. The three dimensional space is also called the xyz-space.
You probably should know how we represent a vector in 3D. Using the same conventions of unit vectors i and j, we just add one more k to represent the unit vector in the z direction (e.g., 2i + 3j – 5k). Everything about a vector in 2D works about the same in 3D. The length of a vector P(a, b, c) follows the Pythagorean relation
And similarly, the distance between 2 position vectors A and B can be found by the equation
Let’s do a little revision on the properties of vectors, scalar multiplication, addition, subtraction & etc. We let a, b and c be 3 vectors, k and h be 2 constants, then we have
(1) a + b = b + a
(2) a + (b + c) = (a + b) + c
(3) a + 0 = a
(4) a + (–a) = 0
(5) k(a + b) = ka + kb
(6) (k + h)a = ka + ha
(7) (kh)a = k(ha)
(8) 1a = a
SCALAR PRODUCT
Scalar product, also known as the dot product, is a multiplication of 2 vectors (a, b, c) and (d, e, f) such that
The scalar product yields an answer in the form of a scalar, which is a value instead of a vector. In trigonometry, it can be represented by the equation
a • b = |a||b| cos θ
I believe all these are not new to you, as you have studied it in Maths T. However, in this section, we will be going quite detail on the algebra of vectors, unlike in Maths T where you focused more on the applications, namely the resultant force / velocity and relative velocity. Let us look at the properties of scalar products. Given a, b and c are vectors, d being a constant, we have
(i) a • b = b • a (commutativity)
(ii) a • (b + c) = a • b + a • c (distributive law)
(iii) (da) • b = d(a • b) = a • (db)
(iv) 0 • a = 0
(v) a • a = |a|2
We say that two vectors are orthogonal to each other when they are perpendicular to each other. Two vectors a and b are orthogonal if and only if a • b = 0. In 3D, we say that a vector a is orthogonal to vectors b and c if a is perpendicular to both b and c.
The component of b onto a (or scalar projection) is the resolved part of a in the direction of b. This means that when we have 2 vectors a and b pointing at 2 different directions, with their tail of the arrow connected to each other, the component of b onto a is the length of the orthogonal projection of b onto a.
We write the notation compa b to represent the component of b onto a, and mathematically, it has the value
and according to the picture above, it is the length of PS.
The vector projection of b onto a is just the vector PS itself. it has the formula
We write the notation proja b to represent the projection of b onto a. Remember that the answer is a VECTOR, not just a VALUE.
For a vector a (ai, aj, ak), The direction ratio is written as ai : aj : ak, whereby your answer could be in the simplest form (divided by its highest common divisor). The direction cosines of the vector a are
respectively.
The angle between the vector and the z-axis can be found using the equation
and therefore you can deduce the angle between the vector and the x-axis & y-axis respectively.
Recalling that the dot product of 2 vectors, a • b = |a||b| cos θ, we can easily find the angle between 2 vectors,
VECTOR PRODUCT
Also known as cross product, the vector product is something new for you, as it cannot exist in a 2D plane. We define the vector product of 2 vectors (a, b, c) and (d, e, f) to be
The cross product yields a vector (it has a magnitude and a direction), which is orthogonal to both the original vectors. In trigonometry, the cross product a × b = |a||b| sin θ.
You can use the right hand rule to determine the direction of the cross product. Point your fingers to the direction of a, curl it towards the direction of b, then your thumb points in the direction of a × b. This information is very important we come to the section on planes.
Different from the dot product, any vector cross itself yields zero.
ḭ × ḭ = 0, j̰ × j̰ = 0, k̰ × k̰ = 0
Or in other words, the cross product of 2 parallel vectors is zero. You can use your right hand rule to verify this. For the unit vectors, you could also get the following results:
We shall now see the properties of the cross product. If a, b and c are vectors and d is a scalar, then
(i) a × b = –b × a
(ii) (da) × b = d(a × b) = a × (db)
(iii) a × (b + c) = a × b + a × c
(iv) (a + b) × c = a × c + b × c
(v) a • (b × c) = (a × b) • c
(vi) a × (b × c) = (a • c)b – (a • b)c
(vii) (a × b) • a = 0
Probably (vi) is hard to remember. (vii) is just the definition of the dot product, where the dot product of 2 orthogonal vectors equals to zero. Also take note that the cross product is not commutative. Reversing the a’s and b’s will result in an extra minus sign.
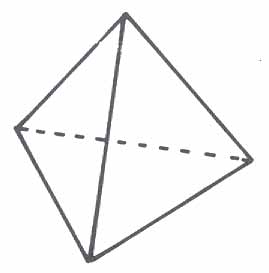
The cross product has many applications, especially in physics. You use the cross product to find the torque, magnetic force and etc. In geometry, we see that the area of a triangle made up by 3 vectors a, b and c is
A scalar triple product of vectors a, b and c is a • b × c. If you might have noticed, you have to do the cross product first before the dot product. If you did the dot product first, then you get a scalar crossing a vector, in which by definition, does not exist. Note also that a • b × c = a × b • c. We could evaluate a • b × c using determinant
Where a = (a1, a2, a3), b = (b1, b2, b3), and c = (c1, c2, c3) respectively. We use the scalar triple product to find the volumes of various solids. Since b × c is the base area of a solid, when dotted with another vector a, it multiplies the area with the cosine of the height. So the formulas for different solids are as below:
1. volume of cuboid & parallelogram:
a • b × c
Not really hard I think. You might probably be asked to simplify an equation by making use of the properties of the cross and dot products. Get used to them, you will use them for the next two sections! ☺


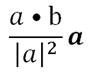
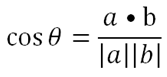









Product of two Vectors
ReplyDeleteProduct of vectors, cross product, scalar product, dot product, vector product, properties of vector product.
http://www.infoaw.com/article.php?articleId=865
thenx a lot .
ReplyDelete