You’ll terribly ‘love’ this section.
Consider how you read your time on the clock. Every time the short hand goes one round, it will be 12 hours. So when the shorthand goes past another hour, it will be 13 hours, and the time might be 13 o’ clock. We know, however that 13’ o clock is actually 1 o’ clock. Same to 25 o’ clock, it still means the same thing. We say that the clock follows a modular system.
Modular Arithmetic, is the calculations of numbers in a modular system. In the clock’s system, it is of modulo 12. When two numbers a and b are congruent to each other in the same modulo, we denote it by
a ≡ b (mod m)
This equation is read as ‘a is congruent to b modulo m’. For example, 13 ≡ 1 (mod 12), this means that 13 is the same as 1 in a modulo 12 system. Note that the main equation is the part on the left hand side, 13 ≡ 1, while the right hand side, (mod 12), tells you that this equation is valid only in modulo 12. This modulo system also has another explanation for it. a ≡ b (mod m) means that a and b give the same remainder when divided by m. Notice that 13 divided by 12 gives remainder 1, while 1 divided by 12 also gives the remainder 1. Or using the mod terminology, we say that
a mod m = b mod m
Take note that a ≡ b (mod m) and a = b mod m both bring different meanings. The latter says that ‘a is the remainder when b is divided by m’.
Now, bringing divisibility in, we say that
a ≡ b (mod m) if and only if m | (a – b)
Can you see that m divides a and b? And if that is the case, a and b actually have a difference of a multiple of m. So this means that, 49 ≡ 37 ≡ 25 ≡ 13 ≡ 1 (mod 12). You just add 12 to the number, you get another number which is congruent modulo 12.
If I convert this notation a ≡ b (mod m) into algebra, it can be written as a = b + km, where k is a constant (try verifying this with the divisibility notation above). So to summarize things up:
When a ≡ b (mod m), then
a mod m = b mod m
m | (a – b)
a = b + km
Before we go into solving linear congruences, we need to know some basic rules of modular arithmetic. These rules below can be proven by yourself, and so try doing it.
If a ≡ b (mod m) and c ≡ d (mod m), then
1. a + c ≡ b + d (mod m)
2. a – c ≡ b – d (mod m)
When in the same modulo m, the addition and subtraction rules work as usual. This will be useful when you are solving simultaneous modular arithmetic equations. This can be proven by using its algebraic form, a = b + km, c = d + lm.
3. ac ≡ bd (mod m)
This is also important, and uses the same method above to prove.
4. ak ≡ bk (mod m)
Where k is a constant, a positive integer. I’ll proof this one here for you:
When a – b = km, then ak – bk = (a – b)(ak-1 + ak-2b + ak-3b2 + … + abk-2 + bk-1), which is a multiple of (a – b). Therefore, ak – bk = lm, where l is a constant, and therefore
ak – bk ≡ 0 (mod m)
ak ≡ bk (mod m)
5. ak ≡ bk (mod m)
The congruence holds even when a constant is multiplied to both sides of the equation. Same proof as 1, 2 and 3.
Next, try proving both the equations below (make use of the information that
a ≡ (a mod m) (mod m):
6. (a + b) mod m ≡ [(a mod m) + (b mod m)] (mod m)
7. ab mod m ≡ [(a mod m)(b mod m)] (mod m)
8. The Simplification Law
If c | a, c | b, c | m, and a ≡ b (mod m), then
To summarize this rule, it means that a constant c can only be divided out from a, b and m if it divides all of them. Provable too.
Here’s another one not to be confused with the former, the cancellation law. If gcd (c,m) = 1, then
9. ac ≡ bc (mod m) ⇒ a ≡ b (mod m)
You can prove this too. Suppose ac – bc = (a – b)c = km. Since gcd (c, m) = 1, c and m have no common divisors, and therefore c | k. Since c divides this constant k, c can be cancelled out, and thus a – b = nm for some integer n. Here we see that a ≡ b (mod m), which was to be shown.
FINDING THE INVERSE
b, the multiplicative inverse of a number a is such that ab = 1. Here, we can find that b is actually the reciprocal of the number a. Here in modular arithmetic, we are going to look for an inverse of a, such that
ab ≡ 1 (mod m)
Let us recall the Euclidean Algorithm. We learnt that we could find gcd (a, m) by dividing the bigger number with the smaller number, and continue to divide the smaller number with its remainder, and so on until there is no remainder. Indeed, we could make use of this information to find the gcd in terms of a linear combination of these 2 integers, such that
gcd (a, m) = m • n + a • b
where n and b are integers. If gcd (a, m) = 1, then an inverse of a exist, and the integer b happens to be the inverse of a. We will see why this is true in the following example:
Find gcd (123, 2347) and write it as a linear combination of these integers, and further find the inverse of 123 modulo 2347.
2347 = 123 • 19 + 10
123 = 10 • 12 + 3
10 = 3 • 3 + 1
3 = 1 • 3
∴ gcd (123, 2347) = 1
Now, to get the linear combination thingy, we have to reverse all of the above equations. Let me rewrite them again:
10 = 2347 – 123 • 19 (1)
3 = 123 – 10 • 12 (2)
1 = 10 – 3 • 3 (3)
Now we will do some back substitution. We want an equation of gcd (123, 2347) (which is 1) to be in terms of 123 and 2347. We start with equation (3), and substitute equation (2), we have
1 = 10 – 3 • (123 – 10 • 12)
= 10 – 3 • 123 + 10 • 36
= 10 • 37 – 3 • 123
Repeating the process with equation (1),
1 = (2347 – 123 • 19) • 37 – 3 • 123
1 = 2347 • 37 – 123 • 706
We have now shown the gcd (123, 2347) in terms of a linear combination of its numbers. This is what we called as the extended Euclidean Algorithm. Here, we find that the inverse of 123 modulo 2347 is –706. We see that
-706 • 123 ≡ –86838 ≡ 1 (mod 2347)
Note that every integer congruent to –706 modulo 2347 is also the inverse of 123, which we find it best to represent the inverse of 123 as 1641, a positive integer less than 2347.
I haven’t tell you why this works. Since gcd (a, m) = 1, and we know that it can be represented as a linear combination 1 = m • n + a • b, we can show that
m • n + a • b ≡ 1 (mod m)
You should understand this equation. If 1 = 3 – 2, then 1 ≡ 3 – 2 for whatever modulo, and that make sense. Here, since m • n ≡ 0 (mod m), as this is obvious, since m divides itself completely, in whatever given n. So in the end, we have a • b ≡ 1 (mod m), which was what we used just now. Note that not all integers have inverses in a particular modulo. It is only in the case where gcd (a, m) such that there will be an inverse.
By the way, the inverse could also slowly be found by trial and error for small moduli. For example, 2 mod 3. Try multiplying the numbers between 1 to 3 to the number 2, and you find that 2 • 2 ≡ 4 ≡ 1 (mod 3). And thus, 2 is the inverse of 2 modulo 3.
SOLVING LINEAR CONGRUENCES
A linear congruence equation has the form
ax ≡ b (mod m)
In which we want to find x. If you can relate this to the section above, it has a solution only if gcd (a, m) = 1. This can be solved by finding the inverse of a. Let’s try an example:
Solve the linear congruence 3x ≡ 4 (mod 7).
We have checked that gcd (3, 7) = 1, and so an inverse of 3 exist, and thus the solution exists. Using the extended Euclidean Algorithm, we get the inverse of 3 as –2. So multiplying –2 to both sides,
-2 • 3x ≡ –2 • 4 (mod 7)
We know that –2 • 3 ≡ 1 (mod 7), and therefore
x ≡ –8 ≡ 6 (mod 7)
substituting 6 back into x, you get the answer correct. Besides, substituting any integer which is congruent to 6 modulo 7, like 13, 20, –8, –1 and etc are also solutions of the linear congruence.
In cases where gcd (a, m) ≠ 1, there are solutions too, only if gcd (a, m) | b, and there are gcd (a, m) solutions. For example,
2x ≡ 6 (mod 8) has gcd (2, 8) = 2 solutions, but 2x ≡ 5 (mod 8) has no solution. Let’s try to solve the linear congruence 2x ≡ 6 (mod 8). You can solve it as follows:
Using the simplification law, you see that 2 divides 2, 6 and 8 and therefore
x ≡ 3 (mod 4)
which is in another modulo system. If you want the solution to be in the same modulo system, then you need to do some modification. By looking at the equation, you know that
x ≡ 3 (mod 8)
is one solution. The other solution is by adding 3 to the new modulo system you get above, which is 4. You get another solution,
x ≡ 7 (mod 8)
So your solution for the linear congruence 2x ≡ 6 (mod 8) is x ≡ 3 (mod 8), x ≡ 7 (mod 8).
This same method applies: When there are 10 solutions, you keep on adding the new modulo system integer value to the existing answer, until you get 10 solutions.
Let’s try another one, 2x ≡ 6 (mod 9). Using rule number 9 above, you can quickly see that gcd (2, 9) = 1, and therefore x ≡ 3 (mod 9). Try not to confuse this one with the one above.
SIMULTANEOUS LINEAR CONGRUENCES
Similar to the one above, now you have 2 congruences with 2 unknowns, under the same modulo. Let’s consider a system of linear congruences with 2 unknowns:
ax + by ≡ k (mod m)
cx + dy ≡ n (mod m)
We first write this in matrix form:
For this system of congruences to have a solution, there must be an inverse for the matrix. This means, that ad – bc must not be zero, and must exist. Let’s multiply the left and right hand side with its adjoint matrix:
Now we get 2 linear congruences,
(ad – bc) x ≡ (dk – bn) (mod m)
(ad – bc) y ≡ (an – ck) (mod m)
and for such linear congruences to have solution, again we must make sure that the equation gcd (ad – bc, m) = 1 holds. With that you can solve the above 2 linear congruences for x and y. This kind of question came out in STPM 2009, my year. Try solving it with the method I just showed you.
QUADRATIC RESIDUE MODULO M
a quadratic residue modulo m has the form
x2 ≡ q (mod m)
You are supposed to solve the equation in terms of x. I don’t know of any short cut to solve such a problem, but one way is to list out all the possible values, draw a table, and find the answer. Example,
Solve the quadratic residue modulo x2 ≡ 2 (mod 7).
Therefore, we conclude that x ≡ 3 (mod 7) and x ≡ 4 (mod 7).
If you have noticed, we could actually solve linear congruences with the above trial & error method too.
If m is very big but divisible, we could break the modulo system up. For example,
x2 ≡ 14 (mod 35)
We can make it into 2 equations, namely x2 ≡ 14 ≡ 0 (mod 7) and x2 ≡ 14 ≡ 4 (mod 5).
Tabulating the table,
x2 ≡ 0 (mod 7) has the solution x ≡ 0 (mod 7).
x2 ≡ 4 (mod 5) has solutions x ≡ 2 (mod 5) and x ≡ 3 (mod 5)
x ≡ 0 (mod 7) means that
x ≡ 0, 7, 14, 21, 28 (mod 35) are solutions of modulo 35.
x ≡ 2 (mod 5) means that
x ≡ 2, 7, 12, 17, 22, 27, 32 (mod 35) are solutions of modulo 35.
x ≡ 3 (mod 5) means that
x ≡ 8, 13, 18, 23, 28, 33 (mod 35) are solutions of modulo 35.
We find the intersections of x ≡ 0 (mod 7) and x ≡ 2 (mod 5), we get
x ≡ 7 (mod 35)
And we find the intersections of x ≡ 0 (mod 7) and x ≡ 3 (mod 35), we get
x ≡ 28 (mod 35)
And our final answer solution is
x ≡ 7, 28 (mod 35)
MODULAR EXPONENTIATION
I don’t think this is in the syllabus, but it is good for you to know. Modular exponentiations are of the form an mod m. You are normally asked to compute it with a very big value of n. For example,
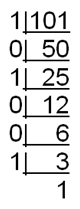
Find 3101 mod 100.
First, do you still remember what are binary numbers? Express the term n in binary form, by keep on dividing the number with 2, writing the remainder by the side. Recall your Form 4 Maths:
So we get 101 = (1100101)2 = 26 + 25 + 22 + 20 = 64 + 32 + 4 + 1
Substituting it back to the congruence,
364+32+4+1 mod 100 = 3643323431 mod 100
Now, we need to tabulate the amounts congruent to 364 332 34 and 31.
32 ≡ 9
34 ≡ 92 ≡ 81
38 ≡ 812 ≡ 61
316 ≡ 612 ≡ 21
332 ≡ 212 ≡ 41
364 ≡ 412 ≡ 81
Now you know all the values, substitute them back into the equation,
3643323431 ≡ 81 • 41 • 81 • 3 ≡ 3 (mod 100)
Spend some time understanding my calculations. If not, just pray that it won’t come out in exams.
CHINESE REMAINDER THEOREM
In the 1st century, the Chinese Mathematician Sun-Tsu asked:
There are certain things whose number is unknown. When divided by 3, the remainder is 2; when divided by 5, the remainder is 3; and when divided by 7, the remainder is 2. What will be the number of things?
This puzzle can be translated into the following question: What are the solutions of the systems of congruences
x ≡ 2 (mod 3)
x ≡ 3 (mod 5)
x ≡ 2 (mod 7) ?
The Chinese Remainder Theorem, named after the Chinese heritage of problems involving systems of linear congruences, states that when the moduli of a system of linear congruences are pairwise relatively prime, there is a unique solution of the system modulo the product of the moduli.
I will omit the proof, because I don’t understand it either. Here are the steps to solve this kind of problems:
Firstly, for a system of linear congruences with different moduli,
x ≡ a (mod m)
x ≡ b (mod n)
x ≡ c (mod o)
We construct a number M being the product of the moduli,
M = m • n • o
Then, we construct a number Mm, Mn and Mo such that they are the product of the all the moduli in the system other than itself. Which means,
Then, find the inverse of Mm, Mn and Mo respectively:
MmM̅m ≡ 1 (mod m)
MnM̅n ≡ 1 (mod n)
MoM̅o ≡ 1 (mod o)
And finally, your answer will be:
Let’s try to solve Sun Tsu’s problem.
x ≡ 2 (mod 3)
x ≡ 3 (mod 5)
x ≡ 2 (mod 7)
M = 105,
M3 = 35 ≡ 2 (mod 3), inverse M̅3 is 2.
M5 = 21 ≡ 1 (mod 5), inverse M̅5 is 1.
M7 = 15 ≡ 1 (mod 7), inverse M̅7 is 1.
∴ x ≡ (2 • 2 • 35) + (1 • 3 • 21) + (1 • 2 • 15) ≡ 233 ≡ 23 (mod 105)
Note that you cannot let M3 = 2, M5 = 1 and M7 = 1, as you will get a total different answer. However, the inverses can be any other number congruent to itself in its particular modulo.
FERMAT’S LITTLE THEOREM
If p is a prime number and a is an integer not divisible by p, then
ap-1 ≡ 1 (mod p)
ap ≡ a (mod p)
This theorem is here for you to identify if a congruence can be solved easily. Similarly, I won’t prove it, so just keep this theorem in mind and use it if needed.
Very hard, isn’t it? That is why Number Theory is known as the “Queen of Mathematics”. Spend some time digesting this section, and figuring out why numbers can be so complicated.☺


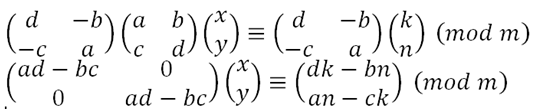


Can you please send me a proof of the Simplification Law? I simply cannot do it by myself.
ReplyDeleteThank you very much for putting this together in this friendly and simple manner. Much appreciated by an ib student a week before the exam :3
ReplyDelete