A theorem is a statement that can be shown true.
A proof is a valid argument that establishes the truth of a theorem.
In this section, I will be showing you 3 main kinds of proof (with tonnes of sub-proofs).
DIRECT PROOF
This proof is very straightforward. A direct proof of a conditional statement p→q, is shown by showing that p is true, then show that q is true. Basically what it means is that you show that something is true, and therefore some other thing follows to be true as well. Let me give you an example:
Show that the sum of 2 odd integers is even.
Did you notice that this is actually a conditional statement? We let p be ‘m & n are odd integers’ and q be ‘the sum of m & n are even’. Putting p→q, we have ‘If m & n are odd, then their sum is even’. So the proof is:
Let m = 2j + 1, and n = 2k + 1, where j and k are integers. Here we can see that m & n are odd. Then m + n = (2j + 1) + (2k + 1) = 2(j+k+1), which is even.
Therefore, the statement is proven valid.
Try to get used to the definition of odd and even integers, being 2k + 1 and 2k respectively, where k is an arbitrary integer (arbitrary means ‘anything’). Actually, when you are asked to prove odd and even integer stuff, it will definitely be a direct proof, and just substitute these definitions in, then you will find the answer. Another case is in proving theorems related to perfect squares, where you use the definition n = k2. One more case is in proving rational and irrational numbers, where you define a rational number n = j/k. All these definitions will help you a lot, and you may use it in the later chapters, like Number Theory…
INDIRECT PROOF
Literally, an indirect proof is a proof that is not direct, i.e. you don’t prove straight using p→q. There are many kinds of indirect proofs:
1. Proof by Contraposition
This proof basically proves the statement p→q using its contrapositive, which is ~q→~p. Example:
Looking at the question, you know you won’t get anywhere if you try to manipulate the first statement, x + y ≥ 2. So what you do is by assuming that ~q is true, which means x < 1 and y < 1. Remember the fact that the contrapositive of a conditional statement has the same truth value as it has! So here we have
Suppose x < 1 and y < 1. Then x + y < 1 + 1, x + y < 2, which is the negation of x + y ≥ 2. Therefore, the statement is proven valid.
2. Proof by Contradiction (Reductio ad absurdum)
What this proof does is to first assume that p is true, and ~q is true (p→~q). You will eventually evaluate ~q and find out that ~p is also true. Now you have p Λ ~p, which is a contradiction (a statement which is always false)! From here, you conclude that p→q. Example:
Prove that the sum of an irrational number and a rational number is irrational.
Putting it in a p→q form, we rewrite the statement as ‘if m & n are irrational and rational respectively, then their sum is not rational’. Now let’s try solving it:
Suppose r is rational and i is irrational, and r + i = s is rational. [p is true, ~q is true]
Then s could be written as p/q for some integers p and q which have no common factors. r could also be written in the form t/u, where t and u are integers with no common factors too. Using some algebra,
which is contradicting, since i is irrational. So it follows that the sum of an irrational number and a rational number is irrational.
3. Vacuous Proof
All you need to do in this proof is to show that p in the p→q statement is false. (Note that when p is false, the statement will definitely be false!) This is used to proof statements like ‘if 2 + 2 = 5, then it will snow in Malaysia’. Won’t come out in STPM, I assume…
4. Trivial Proof
This proof is similar to the above, but here you must show that q is true in the p→q statement. (Once again recall, when q is true, whether p is true or false, the statement still holds!) For the statement ‘if you give me RM1, then the sun will rise in the east’. I don’t need to explain, right?
5. Proof of Equivalence
This proof is for proving statements of the form p↔q, where you need to prove p→q and its converse, q→p. You can use one of the above methods (direct proof, proof by contraposition or contradiction) to solve the p→q and q→p part. Basically this proof is a combination of proofs, and I don’t think I need to elaborate much on this.
6. Proof by Cases
In this proof, you need to proof something using a case by case basis. For example, Prove that |x| + 2 > 0. I won’t show you the answer. All you need to do is use case by case: case 1 where x > 0, case 2 where x < 0, and case 3 where x = 0, substitute the values of x in it, then show that it is true.
7. Exhaustive Proof
This proof requires you to use up all the possibly numbers in that domain, substitute them into the equation to show that it is valid. E.g., Prove that n2 + 1 > 2n, where 0 < n < 5. Just use up all the values n = 1, 2, 3, 4 and substitute them into the equation to prove it. Very straightforward for a small domain of n.
8. Existence Proof
The questions for this kind of proof normally starts with something like ‘show that there exist a…’. There are 2 kinds of existence proof, it can either be constructive or non-constructive. A constructive one will make you find the exact answer to the question, while the non-constructive approach will prove the statement true even without finding a solution. I’ll show you the examples:
Show that there is an integer that can written as the sum of cubes of two integers in two different ways.
This is true as 1729 = 103 + 93 = 123 + 13. [constructive]
Show that the equation x3 + x - 1 = 0 has a solution.
Let P(x) = x3 + x - 1. Then P(0) = -1 and P(1) = 1. Thus (by the intermediate value theorem), the equation P(x) = 0 has a solution which is between 0 and 1. [non-constructive. Interesting isn’t it?]
9. Uniqueness Proof
This proof is an extension of the previous proof. First you show that there is a solution x for the statement P(x). Then you find a value of c which is true for P(x). So lastly, you show that if x ≠ c, then P(x) is false. Example:
Show that if a, b ϵ R with a ≠ 0, there is unique r ϵ R such that ar - b = 0.
Certainly r = b/a satisfies ar - b = 0. [1st & 2nd part]
Next, suppose s, t both satisfy as - b = 0 and at - b = 0. Then as - b = at - b and so as = at. Since a ≠ 0, we have s = t, which means that the solution is unique. [3rd part]
10. Proof by giving a Counterexample
A counterexample is used to disprove something. This is super easy, for example:
Prove or disprove that the product of 2 irrational numbers is irrational.
Using a counterexample, √2 × √2 = 2, which is rational. So the statement is invalid.
All you need to disprove something is to find a counterexample. That’s it.
Mathematical induction is the most common proof that you will use and see in your exams. There are lots of information on this proof in A-level books, so I don’t need to give you too much examples. What mathematical induction does is that it proves that an equation is true for a particular value, we call it the basis. Then we go on to prove that the equation is valid for any value greater than that basis. To sum up, mathematical induction involves 2 steps:
1. The basis step: you proof that the equation is true for n = 0, n = 1 or whatever initial value they give you in the question.
2. The inductive step: you now assume that the equation is true for n = k. Then you try solving the equation in terms of n = k + 1, and show that the relationship holds too. From here you can conclude that by mathematical induction, the equation is true in that domain.
Let me show you an example:
Use proof by induction to prove that
Since
LHS = RHS, we see that the formula is true for n = 1. We assume that the formula is true for n = k, then we have
and letting n = k+1, we have
Hence
is true for all n ≥ 1. [proven]
I will show you some tips on how to solve different kinds of questions. Remember to do A LOT of exercises on Mathematical Induction!
* Questions involving summations
Try to make use of the fact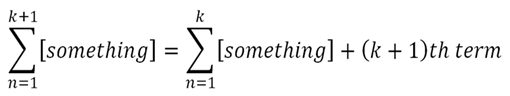
* Questions involving matrices
Try to make use of the fact
Ak+1 = Ak × A, where A is a matrix.
* Questions involving differentials
Try to make use of the fact
* Questions involving recurring terms
Try to make use of the fact
if un + un+1 is divisible by a, then either un & un+1 are both divisible by a, or both not divisible by a.
That’s all for chapter 1. For this section, focus more on mathematical induction, direct proofs and proof by contraposition.
☺

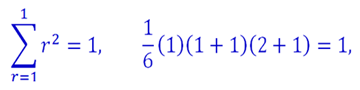

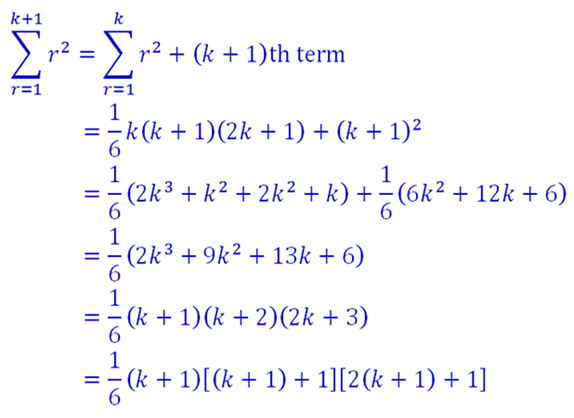
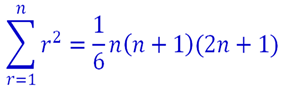

I found a question on mathematical induction which ask us to prove the differentiation of trigonometry, something like this
ReplyDeleted/dx 2e^x sin(x+45'). will we learn this later or we have to learn now, because when we finding for n=k+1, we need to differentiate it but i dunno how to do it.
I did give you an example on differentiation above, didn't I?
ReplyDeleteI mean i dunno how to differentiate the trigonometric because didnt learn before, is the differentiation in maths t cover this part?
ReplyDeleteSure. Probably you might want to read through your Maths T before asking. FMT really does refer a lot back to Maths T.
ReplyDelete