de Moivre’s theorem states that:
for all real values of n,
(cos θ + i sin θ)n = cos nθ + i sin nθ.
This is a very important relationship we need to know about complex numbers. before we start using it, let’s try to prove it first.
PROOF
When n = 1,
(cos θ + i sin θ)1 = cos θ + i sin θ
and so the theorem hold for n = 1.
Now, we assume that the theorem is true for n = k, so
(cos θ + i sin θ)k = cos kθ + i sin kθ
if the equation is true for n = k, it should be true for n = k + 1, and therefore
(cos θ + i sin θ)k+1 = (cos kθ + i sin kθ)(cos θ + i sin θ)
= cos kθ cos θ + 2i cos kθ sin θ – sin kθ sin θ
= cos (k + 1)θ + i sin (k + 1)θ
which is true.
.·. by mathematical induction, de Moivre’s Theorem is true for all integers n > 0.
Let n = –p.
since p = –n, cos (-n)θ – i sin (-n)θ = cos nθ + i sin nθ.
.·. once again, this theorem is proven.
So we see that actually de Moivre’s Theorem is true for all values of n, where n is any integer. We can also show that it is true for fractions, but this is beyond what we can learn. However, one thing to note that if n is not an integer, cos nθ + i sin nθ is only one of the possible values. I will elaborate more on the next post in the section on roots of unity.
The most important thing for this section, is that you need to remember how to prove this theorem, and know how to use it. You will be able to simplify a lot of complex number equations by changing the exponents into just multiplication of numbers.
Another thing you should note is the relations of negative angles.
cos (-θ) = cos θ
sin (-θ) = - sin θ
You will be dealing with all these a lot. It is good to memorize it, and be careful not to make mistakes.
APPLICATIONS
1. I’ll show you an example how de Moivre’s Theorem help you in proving trigonometric identities.
Express sin 3A in terms of sin A.
sin 3A = Im (cos 3A + i sin 3A) [here, “Im” means imaginary, while “Re” means real.]
= Im (cos A + i sin A)3
= Im ( cos3 A + 3 cos2 A i sin A - 3 cos A sin2 A – i sin3 A)
= 3 cos2 A sin A – sin3 A
= 3 sin A – 4 sin3 A
Okay, I need to explain this. Here, we are trying to project the term sin 3A in terms of a complex number, which can be dealt with using de Moivre’s Theorem. So sin 3A, is actually the imaginary part of cos 3A + i sin 3A, and we put the “Im” there because sin 3A belongs to the imaginary part (this means that if our question was cos 3A, we have to put “Re” in front of it instead). We evaluate it, and when we remove the “Im” sign, we remove all the real parts (terms without the ‘i’), leaving the imaginary part without the ‘i’ in it. Try using this method to solve cos 3A, you will understand more by then.
2. If we set z = cos θ + i sin θ, then
From here, you can further deduce that
With all these, we can do the above example backwards.
Express sin3 A in terms of sines of multiple angles.
That’s all this time. Try doing lots of exercises on this kind of questions, it might get very complicated when it’s greater than power of 3. ☺



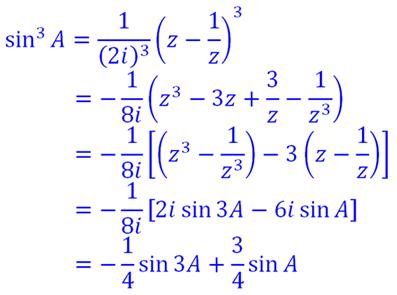
[2-√3i]^6, i saw this question in one of the reference book, how can i simplify it with de Moivre's theorem? i get decimal places for the θ.
ReplyDeleteYou should get √7^6(cos 6 (tan^-1 (-√3/2))+i sin 6 (tan^-1 (-√3/2))). It will then be -143 +180√3i
ReplyDeleteReally thank you..this helps alot..
ReplyDeleteHow to solve 5z^4 - z^3 + 4z^2 - z+ 5 = 0 by using de Moivre theorem?
ReplyDelete