Generally, Taylor series has a lot of uses. We can use it to do one of the following:
A. DERIVE A GIVEN FUNCTION
You were given a list of Maclaurin series in the last section. Now I show them to you again below:
These are not all though. You can still find and derive the Taylor or Maclaurin series of other functions like sin-1 x, coth-1 x or lg x2. The method is the same, by listing down the Taylor or Maclaurin series of the functions. For example,
sin-1 x = a + bx + cx2 + dx3 + ex4 + …
and you substitute x = 0 to get a. To get b, you differentiate once and substitute x = 0, and c, differentiate twice, and etc. The coefficients a, b, c and so on might not have a certain order like the functions listed above, but at least you have a reasonable polynomial to estimate the function in the absence of a calculator.
Besides, you could also combine more than 2 functions to find a new Taylor series for them. For example, (1 + x)2 cos x can be derived from
Adding and subtracting of functions (like sin x + cos x) or even substitution of variables (like e8x or sin x2) can be easily derived too.
B. DIFFERENTIATE AND INTEGRATE THE SERIES TO GET OTHER RESULTS
Did you notice that the laws of calculus also obeys the rules of power series? Taking cos x for an example, differentiating both sides, gives
This is a very useful information. You can speed up the calculations if you were asked to derive the series of a function which relates to on of the known functions above. By the way, if you were able to find the listing of the polynomials, you would want to learn how to find the summation notation of the derived series as well. Read through your Maths T Sequence & Series, and try to make use of the knowledge you learn there.
C. FINDING LIMITS OF FUNCTIONS
When you are asked to find the limit of a complicated function as x → 0, you can actually make use of the Maclaurin series of the function. For example,
To help you, you might want to learn L’Hôpital’s rule as well. This rule comes really handy in this situation, it states that if f(a) = 0, g(a) = 0, and g’(a) ≠ 0, then
Use this rule when you get a 0/0 results. Remember that this rule only holds if the f(a) = 0 thingy is true.
D. SOLVING DIFFERENTIAL EQUATIONS NUMERICALLY
I believe you already know what are differential equations, just that you only know how to solve a little of them. So here, we are trying to estimate and represent a set of differential equations as a Taylor series, and thus try to estimate the function for values x close to a, when expanded at x = a. I’ll show you an example:
Find the Taylor’s series solution for y up to and including terms in x4 for the differential equation
Hence, find y correct to 9 d.p. when x = 0.01.
That’s all for this chapter. Still remember the derivations of Poisson Distribution? You probably could explain to your friends now using your knowledge on Power Series. ☺



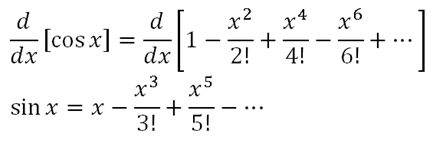




No comments:
Post a Comment