The hyperbolic functions, of which there are six, are so named because they are related to the parametric equations for a hyperbola.
The 2 main hyperbolic functions are sinh x and cosh x (and so now you know what the ‘hyp’ button on your calculator is for). The hyperbolic functions are actually functions of the natural exponents ex through the following equations:
We now relate the hyperbolic functions with the hyperbola. The equation for the hyperbola is
We let
x = a cosh u
y = b sinh u
We find that cosh2 u – sinh2 u = 1, which is true (This can be proven by substituting the ex into the equation). Now that we have 2 hyperbolic functions, we use it to further derive a few other functions following a similar convention which the trigonometric function uses:
All these 6 hyperbolic functions have their special pronunciation. sinh is read as ‘shine’, cosh as ‘cosh’, tanh as ‘than’, sech as ‘sheck’, csch as ‘co-sheck’ and coth as ‘cough’.
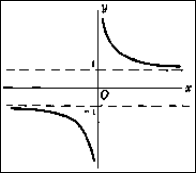
Now we shall see the graphs of the 6 hyperbolic functions. Note that they are all derived from the exponential function:

cosh x sinh x tanh x
Their domain and ranges are as follows:
Now that you know the basic information of these functions, it’s time to memorize formulas. But before you start, I need to introduce a special rule which makes the memorizing easier.
The Osborne’s Rule states that to change a standard ordinary trigonometric identities into the equivalent standard hyperbolic identity, change the sign of the term which is the product of two sines, and substitute the corresponding hyperbolic functions. This means that if you remember all the trigonometric identities, you can remember the hyperbolic identities. Please note that all the trigonometric formulas which have the periodic characteristics (for example, the R formula and the phase shifts) do not apply to hyperbolic functions, as they are not periodic.
For each case, you should be able to derive them. Proving them is simple, just plug in the ex relation into it and you are sure to get it.
The formulas and identities are as follows:
Besides all these formulas, you should also know the relations between hyperbolic functions and trigonometric functions. Use the following to derive those for tanh x, sech x, csch x and coth x too. Bear in mind that i × i = –1.
To prove this, you will need to wait till you learn Power Series in Chapter 7.
Easy to memorize, isn’t it? Exam questions normally focus on proving stuff, and probably sketching graphs too. Be very careful not to make mistakes. ☺
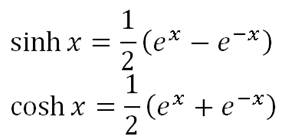









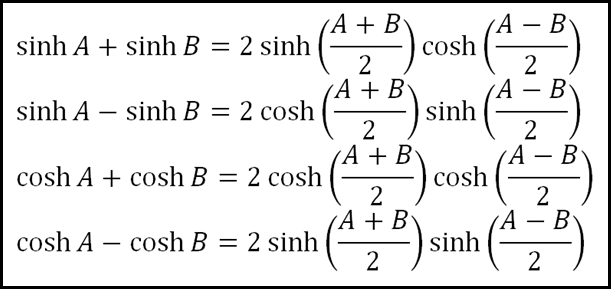
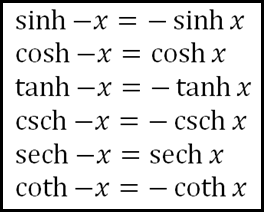
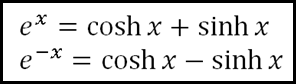
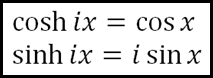
I took a look over this blog and find it more useful for students.Hyperbolic functions occur in the results of some linear differential equations, for example the equation defining a catenary, of some cubic equations, and of Laplace's equation in Cartesian coordinates.The hyperbolic functions take real values for a real argument called a hyperbolic angle. In complex analysis, they are rational functions of exponentials and meromorphic.
ReplyDeleteParametric Equations