This is my favourite chapter. ♥
The χ2 Distribution (read as ‘kai-squared’, written as ‘chi-squared’) is just another new distribution that we will be learning today. This distribution mainly helps us to see or analyse, whether a particular population fits into a certain distribution (Binomial, Poisson, Normal etc). For example, if you have a list of the height of the students in your school, you want to know whether the list fits a normal distribution. You conduct a test of goodness-of-fit. Then probably you also want to know whether the weather during the football match affects the results of the same football team. You conduct a test of independence. These tests have the similar format of how a hypothesis test is conducted, but before I go into it, let me introduce this distribution and its attributes.
The χ2 Distribution has one parameter, ν, pronounced ‘new’, known as the number of degrees of freedom. The shape of the distribution is different for different values of ν. Take a look at the graph below:
As ν increases, the curve looks rounder, and tends to start from zero. The curve is positively skewed for ν > 2, and when ν is large, the distribution is approximately normal. If we are using a chi-squared distribution with 5 degrees of freedom, we say that we are using a χ2(5) distribution, or X2 ~ χ2 (5).
The table for the critical values of the χ2 distribution looks something like this:
Unlike hypothesis testing and confidence intervals, which you might look for 2 tailed, upper tail or lower tail tests, you are only required to look for the upper tail critical value for the χ2 distribution. However, the similarity with hypothesis testing is the significance levels, which are 5%, 10%, 1% or so.

The critical region, as before, is the upper blue region shown in the graph, and the boundary of the critical region is called the critical value. For a 5% level of significance, the critical value is written as χ25% (ν), where the value depends on ν. So looking at the graph, χ25% (5) has the value of 11.070.
Before I introduce to you the test statistic, I’ll give you an illustration on how they come about. Suppose that I give you a table below.
I told you that these were the random numbers generated by a calculator. However, you doubt whether it is truly random. When we say that the values are random, it means they have equal probability of appearing. So this means, the frequency should follow a uniform distribution, with every digit appearing with a frequency of 10 each.
So the observed frequency O is your experimental results, while the expected frequency E is what you think it should be. So your test statistic X2 is
Let’s try to understand this expression. The term (O - E)2 will become very large, if the expected and observed frequency are very far apart (like for the digit 0). Dividing with E gives us the percentage difference. So this tells us that, if X2 is very big, then you know that it is definitely not the correct distribution (in this case, it is not uniformly distributed). But if X2 is close to 0, then we can say that the data definitely follows that distribution.
This formula for X2 is correct for any value of ν, except when ν = 1. We need to use the Yates Correction,
Now you might be wondering how do we determine the value of ν. ν can be found through the formula
ν = number of classes – number of restrictions
The number of classes is the number of columns you have in your table. For the one above, it has 10 classes. The number of restrictions depends on whether the mean or variance is known and whether the sum of observation frequency is known. In a uniform distribution, there is only 1 restriction, that is ΣO = 100. We will get into the details in the next post.
Now that you know the basics about the χ2 distribution, we shall proceed to learn how to make tests of goodness of fit, in the next section. ☺



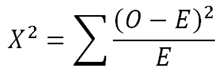
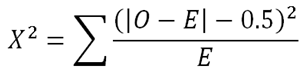
No comments:
Post a Comment