To define a certain distribution, be it Binomial, Poisson or Normal, you need to know their population parameters. And of course, if you don’t know the parameters before hand, you would want to use sampling to estimate it. This estimate is unbiased if the average (or expectation) of a large number of values taken in the same way is the true value of the parameter. The best way to estimate these parameters is by using one with the smallest variance.
So here in this section, we are focusing on point estimates. We estimate that the parameters are those points or data that we collected through the samples. Look at the 3 equations below.
We denote an unbiased estimate with a cap. So the unbiased estimate of the proportion of success in the population, the population mean and population variance are denoted by p̂, μ̂ and σ̂2 respectively. It is found that, the best unbiased estimate for the population proportion and population mean, are the sample proportion ps and the sample mean x̅ themselves. However, the best unbiased estimate for the population variance is denoted differently, with the above formula. The formula for the expected variance can also have the following forms:
That is all you need to know about this section. Let me give you a short example:
The concentrations, in milligrams per litre, of a trace element in 7 randomly chosen samples of water from a spring were
240.8, 237.3, 236.7, 236.6, 234.2, 233.9, 232.5
Determine the unbiased estimates of the mean and the variance of the concentration of the trace element per little of water from the spring.
To answer this question, we need to make use of our calculator. Set your CASIO 570MS to SD mode, and input all the data into it, by pressing the individual numbers in, every time followed by the DT button, until you finished inputting everything. Next, you press
shift+S-VAR. It gives you the option of x̅, xσn and xσn-1. The first one gives you the unbiased estimate of the mean, while the last one will give you the unbiased estimate of the standard deviation. Just show them a little working even though you know the answers straight away:
Easy isn’t it? I know you don’t expect something easy to come out in exams. Probably you should read more about the next section. ☺

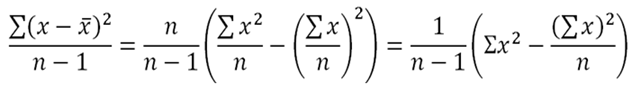

No comments:
Post a Comment