You previously learnt how to formulate a null and alternate hypothesis, and determine your test statistic and test value. With these information is still not enough. We shall now proceed to setting the significance level, and determining the critical region.
When making a hypothesis test, you have to make a decision about the significance level, which is the value of the probability that is considered to imply an unlikely or rare event. As a guide, events that have a probability of 5% or less are regarded as unlikely and events having a probability of 1% or less are regarded as very unlikely. Other significance level used are 10% and 2% respectively. Try not to confuse this with what you learned in the previous chapter, which was confidence intervals, in terms of 90+%.
Let’s say, in a test of 10 true-false questions which were written in Hindi, your friend got 6 questions correct, and you want to know whether he was guessing, or he really studied Hindi. You formulate the hypotheses as below:
H0: Your friend is guessing. He makes use of the 50% luck.
H1: Your friend seriously studied Hindi before. He scores more than 50%.
Mathematically, this is a binomial problem again, X ~ B(10, 0.50).
H0: p = 0.50
H1: p > 0.50
Notice that the expression for H0 always has an ‘=' sign, while H1 should have either <, > or ≠ signs. To start our test, we need to define our significance level. We can say, for example, that we want to test at the 5% level, that he could have obtained this score by guessing all the answers. We can also choose to test at 1% level or 10% level, and obviously, you might get different results.
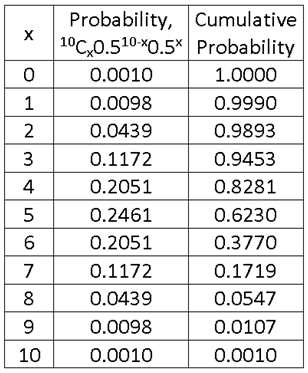
So from here you can see that in the last section, you can’t get any answer if you don’t set a significance level. You can’t say how much you have improved in your running, unless you state that “an increase in 5% is significant”, or “if I run faster by 10%, then there is significant improvement”. With this significant level, then only our hypothesis could be done. For the example above, say, we want to test it at 5% level. We first need to find out the probability of how many questions he get correct. We plot a cumulative binomial distribution
X ~ B(10, 0.50).
Notice that it is a decreasing cumulative Binomial plot.
This curve tells us the probability he gets ≥ n questions correct. So we see that, there is 99.9% probability that he gets at least one question correct, and 62.3% probability that he gets at least 5 questions correct etc. Even if your friend gets 8 questions correct, there is 5.5% probability that he is guessing, which is still above our required significance level. So here, if he gets 9 questions correct, it must be really a rare event, as he has only 1.1% probability of getting this score if he was guessing. We say that the numbers 9 and 10 lie in the critical region, which is the group of observations that are considered to be unusual or unlikely (rare) events. We also say that number 9 is the critical value, or cut-off point, since anything above it is considered a rare event.
So what can we conclude from here? We can see that if your friend got 0 to 8 questions correct, we have no evidence, saying that he did studied Hindi, as these are not rare events (they are > 5% probability). We say that the null hypothesis H0 is not rejected, which is the case. But if he gets 9 or 10 questions correct, we say that there is evidence, at 5% significance level, that your friend did study Hindi. In other words, the null hypothesis H0 is rejected in favour of the alternative hypothesis H1.
Notice that if we did a 10% significance level test, number 8 now lies in the critical region! So this is actually very subjective, and it really depends on you (or the question in your test paper) to determine what is considered significant and what is not.
Let me sum up what you understand about hypothesis testing by now:
1. To test something, you need to first define your null hypothesis H0, something that is
claimed, or happening.
2. Then you define your alternative hypothesis H1 just in case H0 is not true.
3. Find your test statistic, test value.
4. Try to identify what kind of distribution it is from.
5. Determine a significance level to reject or accept the claim.
6. Plot or use a given cumulative distribution to find the critical regions.
7. Determine whether the test value lies in the critical region. If yes, then H0 is rejected. If not,
H0 is accepted.
This is only a rough idea of how a hypothesis is about. You might still be a little confused about what is happening, I have to apologize for that, because I break down this chapter in quite a weird way. We will be going ALL INTO it in the next section, where the calculations come it. ☺

No comments:
Post a Comment