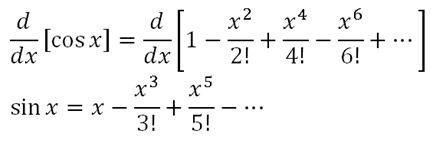In this section, we will be learning how to solve second order linear differential equations, both homogeneous and non-homogeneous.
HOMOGENEOUS CASE
A second order homogeneous linear differential equation has the form
where a, b and c are constants. We first give a smart guess (ansatz) that the solution has the form y = Aenx, where A is a constant, and n is an integer. Differentiating it yields
and once we substitute all equations into the differential equation, and eliminating Aenx, we get a quadratic equation of the form
which we call as the auxiliary equation. From here we can see that y = Aenx is indeed a solution for the 2nd order differential equation, provided that the value of n satisfies this equation. Once we find the values of n, we can thus write down the general solution of the differential equation.
However, the equation will give you 3 outcomes, which is either it has 2 distinct roots, 2 equal roots or 2 complex roots.
Case 1: 2 Distinct Roots
In this case, suppose the auxiliary equation gives you 2 roots n1 and n2. your answer for y will be in the form of
Remember that your initial guessed solution for the differential equation was y = Aenx? Notice that if y = Aenx and y = Bemx both are solutions of the the differential equation, then the sum of both the solutions, y = Aenx + Bemx is also a solution for the differential solution. That is why, our solution for y is the sum of both solutions. You may want to prove it. Given the differential equation
You find the auxiliary equation to have the values n = –1, –2 respectively. Do try substituting y = Ae-x, y = Ae-2x and y = Ae-x + Be-2x into the equation. All of them are consistent, aren’t they?
Case 2: 2 Equal Roots
Suppose your auxiliary equation gives you only one value of n. Your answer will be in the form of
When there is a repeated root, you multiply it by x. Try recalling the connection of this chapter with what you learnt in the chapter Recurrence Relations.
Case 3: Complex Roots
Suppose you get 2 complex roots, m + in and m – in. Your answer will then be in the form of
Notice the second line of the equation. Remember the fact that
e(m+in)x = emx(cos nx + i sin nx), and you get y = emx[ (A + B)cos nx + i(A – B)sin nx ], in which you represent the terms (A + B) and i(A – B) as C and D respectively. You will be surprised that D is actually a real constant, so somewhere on the way, A and B must have been complex.
As I said, these are the forms of general solutions that you can get. To get a particular solution, you need to have an initial condition, something like when y = 1, x = 0 or so. The particular solution eliminates the constants ABCD, and gives them in terms of real numbers instead.
NON-HOMOGENEOUS CASE
A second order non-homogeneous linear differential equation has the form
Again, a, b and c are constants, and f(x) is a function of x, which is either a polynomial, a constant, an exponential function, a cosine or sine function, or a combination of any 2. Functions like tan x, sinh x or ln x will be out of your syllabus, in which the solving of these kinds of differential equations will require the Method of Variation of Parameters. Try google for it if you want to know more.
The solving method is easy. First you separate the differential equation into 2 parts. You let the first part = 0,
and this is solved just as above, by finding the auxiliary equation and then representing the answer in the form of y = g(x) = Aenx + Bemx. This solution is called as the complementary function (CF). The other part f(x) will have the solution y = h(x), which is called as the particular integral (PI). Remember that the sum of solutions is also a solution, so our final answer will be
y = g(x) + h(x)
Since you already know what to do with the CF, we will introduce methods to solve the PI below, which depends on what h(x) is.
Case 1: h(x) is a Polynomial Function
You should just substitute the PI as a polynomial function. For example,
You already know the CF from above, which is y = Ae-x + Be-2x. Then to find the PI, you let
y = Ax2 + Bx + C, according to the degree of the polynomial. Differentiating, you get
Substituting it back, we get 2A + 3(2Ax + B) + 2(Ax2 + Bx + C) = x2 + 4x –3. Solving for ABC, you get A = 1/2, B = 1/2, C = –11/2. So in the end, our PI is
and the general solution, being the sum of the CF and the PI will be
Try not to get confused with the constants of the CF and the PI, in which here, I have 2 A’s and 2 B’s. I would suggest you that you should name the constants for the PI as C, D and E instead. This rule applies for any polynomial of degree n. However, there is an exception, when your auxiliary equation has a root n = 0. Since Ae0 = A, you already have a constant term in the CF. So for your PI, you need to multiply your solution with an extra x. So if your
f(x) is 4x + 3, your PI should be Bx2 + Cx instead of Bx + C. Similarly, you can guess that if the CF has a double root n = 0, you will then multiply your PI with x2. Try relating this information with the chapter on Recurrence Relations.
Case 2: h(x) is an Exponential Function
This is easy. If f(x) = 5e2x, our PI will be just y = Ce2x. Just differentiate y to get dy/dx and d2y/dx2, substitute it into the equation, and find A. Again in this case, there are exceptions. If your CF already has a term Ae2x, then like the above, you multiply x in front of the PI to give you y = Cxe2x. If your CF is y = Ae2x + Bxe2x, then your PI will be y = Cx2e2x, multiplying x2 this time. Not hard I think. If you are given
Your CF is the same, y = Ae-x + Be-2x. Your PI will be y = Cex + Dxe-2x, and you should further solve the equation yourself.
Case 3: h(x) is a Cosine or Sine Function
If f(x) = 5sin 2x, or f(x) = 4cos 2x, or f(x) = 6sin 2x + 7cos 2x, your PI will be the same, which is y = Ccos 2x + Dsin 2x. Notice that whether you have only sines or only cosines, you still have to come up with both cosines and sines for your PI. The reason is simple, if you only come up with one of them, your solution is not solvable. Again, there is an exception, which is when your auxiliary equation might have totally imaginary roots, which happens to give your CF a sine or cosine function of the same form. As usual, just multiply an x in front of your PI. For example,
You get an auxiliary equation of n = ±4i, CF of y = A cos 4x + B sin 4x. So, your PI should be in the form of y = Cxcos 4x + Dxsin 4x. Differentiate it (might be complicated), substitute it, find constants C and D, and give the general solution by adding the PI and CF. Should be straight forward.
Combinations of functions, like f(x) = x cos 3x, f(x) = xe4x, f(x) = e4xsin 3x shouldn’t be hard for you to solve. The basic rule is if your CF already has a solution with the same form as f(x), then just multiply x to that term. If it doesn’t work, multiply x2 then.
SUBSTITUTION
If you could recall what you learned in Maths T, you have already learned how to use the substitutions v = ax + by and y = vx to transform a complicated-looking differential equation into one that is solvable. You can apply those skills in 2nd order differential equations too. Other kinds of substitution include x = u0.5, u = xy, but I want your attention on solving differential equations of the form
You need to use the substitution
From here, find dy/dx and d2y/dx2 by using the chain rule.
Which in the end, gives you a differential equation of the form
which is solvable.
PROBLEM MODELLING
Seriously, I have looked through many books, but none of them really teach us about modelling for 2nd order differential equations. You should be familiar with modelling of 1st order differential equations though. So here, I have no choice but to introduce to you some university level stuff.
1. LRC Circuits
The potential differences of an inductor, a resistor and a capacitor are denoted by
So this means that the total voltage across the 3 elements put in series is equals to
I assume you know that L, R, C, and Q means inductance, resistance, capacitance and charge respectively. Here we see that the voltage V is a function of time, which makes it a non-homogeneous 2nd order linear differential equation. Solving the differential equation means finding an equation which relates the charge to time.
2. Oscillators
Remember in physics that a simple harmonic oscillator has the equation of
mẍ + kx = 0
where m is the mass, and k is the spring constant. Notice that this is a 2nd order differential equation! Solving this makes you find x in terms of t. A damped oscillator has an extra term in it,
mẍ + bẋ + kx = 0
where b is the drag constant. A forced oscillator, in turn would be
mẍ + kx = F(t)
where the force F is a function of time, probably a sine or cosine function. You could have guessed it, that a forced damped oscillator would be
mẍ + bẋ + kx = F(t)
With these information, you are able to model a second order differential equation once you know all the factors m, b, k and F.
There are a whole lot more of physics equations which requires differential equations, like the famous Schrödinger’s Equation and other higher level stuff, which requires higher level physics. I better stop here before I turn this into a physics lecture instead.
This chapter really isn’t hard to understand, and neither too hard to solve. The only problem is that you can get careless and make mistakes. I got a B+ last time for my Further Mathematics T paper 1 because I made a silly mistake in a question on Differential Equations, and it was 12 marks gone! Now that you know everything about differential equations, hope you will be more confident in exams. ☺